1. FEJEZET: Bemelegítő feladatok
Feladat: 1.1. Hányféleképpen írhatunk be egyet-egyet a
10,
13,
30,
39,
100,
110,
330 számok közül a
□,
▵ jelek
helyére úgy, hogy teljesüljön a
□
▵
=
1
3
összefüggés?
Feladat: 1.2. Írjunk a
□,
▵ jelek helyére egy-egy számot
többféleképpen is úgy, hogy teljesüljön az alább megadott
összefüggés!
a)
□
8
=
▵
6
b)
□
5
=
▵
10
c)
□
3
=
4
▵
d)
15
□
=
21
▵
e)
340
□
=
240
▵
Feladat: 1.3. Egyszerűsítsük az alábbi törteket! Adjuk meg a tovább nem
egyszerűsíthető alakot!
a)
486
48
b)
108
144
c)
169
182
d)
340
85
e)
121
1001
Feladat: 1.4. Végezzük el az alábbi műveleteket számológép használata nélkül! Az
eredményt tovább nem egyszerűsíthető tört alakjában adjuk meg!
a)
7
36
+
11
45
b)
3
98
+
11
21
c)
5
22
-
8
33
d)
2
21
+
1
12
+
3
28
e)
1
10
+
1
15
+
42
1260
f)
50
91
-
35
49
+
3
26
g)
50
91
-(
35
49
+
3
26
)
Feladat: 1.5. a)
1
6
·
3
5
b)
2
98
·7
c)
2
98
:7
d)
24
121
·
77
63
e)
36
175
·
125
81
f)
38
45
:
18
5
g)
24
72
+
4
17
·
51
6
h)
(
24
72
+
4
17
)·
51
6
i)
1
2
-
162
1001
·
143
45
j)
(
1
2
-
162
1001
)·
143
45
k)
1
7
·
35
10
·
19
4
·
72
121
·
143
57
Feladat: 1.6. [
108] A
MALOM szó egy ötjegyű számot helyettesít. Azonos betűk azonos
számokat különböző betűk különböző számokat jelentenek. A betűknek
megfelelő számok mindegyike prímszám, az öt szám összege is
prímszám. Prímszám továbbá a
MA és a
MLO két ill. háromjegyű
szám. Melyik lehet ez az öt szám?
Feladat: 1.7. [
108] Marci három dobókockával játszott. Egyik dobása után örömmel
mondta nővérének, Sáriak: ,,Képzeld, sikerült mindhárom kockával
prímet dobnom, s ezek összege is prím, mégpedig 10-nél nagyobb!"
Sári ezt válaszolta: ,,Akkor biztosan van köztük kettő, amelyiken
ugyanazt dobtad!"
Igaza volt-e Sárinak, s miket dobhatott Marci, ha állítása igaz
volt?
Feladat: 1.8. Adjunk meg két olyan szomszédos pozitív egész számot, amelyek
egyike sem osztható 15-tel, de a szorzatuk osztható 15-tel!
Feladat: 1.9. A nyilak egy-egy számmal való szorzást jelölnek. Az egyforma
nyilak ugyanazzal a számmal szoroznak. Írjuk be a hiányzó
számokat!
|
3 ⇒ ...... → ...... ⇒ ...... → ...... ⇒ 600
|
Feladat: 1.10. Gyűjtsük össze az alábbi számok osztóit és mindegyik osztóhoz
írjuk fel, hogy hányszor van meg a számban!
a)
36
b) 64
c) 65
d) 108
e) 130
Feladat: 1.11. A 36, 64, 65, 108, 130 számok hányféleképpen írhatók fel két
tényező szorzatára, ha a tényezők
a) pozitív egészek és számít a sorrendjük?
b) tetszőleges egészek és számít a sorrendjük?
c) pozitív egészek és nem számít a sorrendjük?
d) tetszőleges egészek és nem számít a sorrendjük?
Feladat: 1.12. Rajzoljunk minél többféle
a)
28
b) 36
egybevágó kis négyzetből álló téglalapot!
Feladat: 1.13. Hány különböző téglatest készíthető
a)
28
b) 36
egybevágó kis kockából?
Feladat: 1.14. Mely
1-nél nagyobb számnak van
a) a
legtöbb
b) pontosan 3
100-nál nem nagyobb pozitív
többszöröse?
Feladat: 1.15. Mely kétjegyű számoknak van a
a) legtöbb
b) legkevesebb
osztója?
Feladat: 1.16. Fel lehet-e írni a
a) 210-et
b)
300-at
két szomszédos egész szám szorzataként?
Feladat: 1.17. [
98] Egy háromjegyű páratlan számról meg kell állapítani, hogy
prímszám-e vagy összetett. Okos Berci 3-tól 31-ig nem talált
osztót. Ezek után azt mondta, hogy a szám biztosan prímszám. Igaza
volt? Miért?
Feladat: 1.18. [
111] Igaz-e, hogy a 330-at fel lehet bontani
| a) Két páros szám összegére? | b)szorzatára? |
| c) Két páratlan szám összegére? | d)szorzatára? |
| e) Két 3-mal osztható szám összegére? | f)szorzatára? |
| g) Két 3-mal nem osztható szám összegére? | h)szorzatára? |
| i) Egy hárommal osztható és egy
hárommal | |
| nem osztható szám összegére? | j)szorzatára?
|
Feladat: 1.19. [
52] Meg lehet-e adni négy egész számot úgy, hogy összegük és szorzatuk
is páratlan legyen?
Feladat: 1.20. Három egész szám összege
a) 2002;
b) 2003.
Lehet-e 1 a három szám szorzatának utolsó
jegye?
Feladat: 1.21. [
108] Van-e három olyan egymást követő, 0-tól különböző természetes
szám, amelyek összege prím?
Feladat: 1.22. [
108] Van-e négy egymást követő prímszám, amelyek összege is prím?
Feladat: 1.23. Rendezzük két csoportba az 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 számokat
úgy, hogy az egy csoportban levő számok
a)
összege
b) szorzata
egyenlő legyen!
Feladat: 1.24. Keressünk 7 olyan egymást követő pozitív egész számot, amelyek két
csoportba oszthatók úgy, hogy az egyik csoportba tartozó számok
a) összege
b) szorzata
ugyanannyi, mint a másik csoportba tartozóké!
Feladat: 1.25. [
118] Töltsük ki az az
1. ábrán látható négyzeteket
az 1, 2, 3, 4, 5, 6, 7, 8 számokkal úgy, hogy egy-egy egyenes
mentén a számok szorzata a kis körben levő számmal legyen egyenlő!
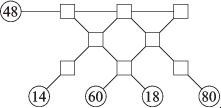
1. ábra
Feladat: 1.26. [
108] Melyek azok a háromjegyű prímek, amelyek számjegyeit összeszorozva
10-et kapunk?
Feladat: 1.27. Jóska köralakú futópályán edz. A pálya hossza
390m.
a) Hétfőn 9 teljes kört és még 120 métert futott.
Összesen hány
m-t futott?
b) Kedden 11 teljes körhöz még 120 méter hiányzott, de
ott elfogyott a szufla. Így hány
m-t futott?
c) Szerdán pontosan
5km-ig bírta. Hány teljes kört
tett meg? Ha a leggyorsabban akar eljutni kiindulási helyére,
akkor melyik irányba kell mennie és hány métert kell megtennie?
d) Csütörtökön már a verseny helyszínén edzett, ahol csak
380m hosszú a pálya. Itt is épp
5km-t futott. Ez hány teljes
kört jelentett? Most melyik irányban sétáljon a pályán, hogy a
legrövidebben visszajusson a rajtvonalhoz? Hány métert kell
megtennie?
e) Pénteken csak az edzőpálya volt szabad. Ezen Jóska
6km-t futott majd ugyanabban az irányban még
150m sétált, mert
így jutott a pályán a leghamarabb a starthoz. Milyen hosszú
lehetett a pálya? (Feltehetjük, hogy
m-ben 450-nél kisebb 10-zel
osztható szám.)
Feladat: 1.28. Számlétra
Két játékos felváltva mond pozitív egész számokat. 1-gyel, 2-vel
vagy 3-mal lehet kezdeni és minden további lépésben is az ellenfél
által kimondott számnál 1-gyel, 2-vel vagy 3-mal nagyobb számot
lehet csak mondani. Az nyer, aki kimondja a 21-et.
A kezdőnek vagy a másodiknak szóló játékosnak kedvező-e a játék?
Mi a nyerő stratégia?
Feladat: 1.29. Szorzójáték
Két játékos felváltva mond 24-nél nem nagyobb pozitív egész
számokat. Korábban már kimondott számot egyikük sem mondhat. Az a
játékos nyer, aki olyan számot mond, amelynek szorzata az előzőleg
elhangzottal épp 24.
A kezdőnek vagy a másodiknak szóló játékosnak kedvező-e a játék?
Mi a nyerő stratégia?
Feladat: 1.30. Készítsünk algoritmust, ami előállít egy
20×20-as
szorzótáblát!

