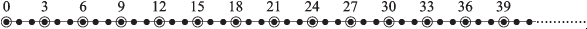7. FEJEZET: Maradékos osztás
Feladat: 7.1. Soroljuk fel az alábbi halmazok elemeit!
H={4k+1|k egyjegyű pozitív egész
}
G={3n-1|n∈Z,
n2
<30}
Feladat: 7.2. [
63] A számsorban a 0-tól kezdve minden harmadik szám osztható 3-mal.
Ezt az
1. számegyenesen is ábrázoltuk.
1. ábra
Egyetlen kifejezéssel is felírhatjuk az összes 3-mal osztható
számot:
3k, ahol
k természetes szám.
a.1) A
3k kifejezés melyik 3-mal osztható számot adja
meg, ha
k=0;
k=3;
4k=123?
a.2) Milyen
k-t kell választani ahhoz, hogy megadjuk a
9000-et?
b.1) Az
1. számvonalon
jelöljünk meg
x-szel néhány olyan számot, amely 3-mal osztva
1-et ad maradékul! Adjuk meg ezeket a számokat egyetlen
kifejezéssel!
b.2) Hányadik helyen áll a most megjelölt számok
sorozatában az 511 és a 9010?
b.3) Melyik szám áll a 128. helyen?
c.1) Milyen tulajdonságúak az eddig meg nem jelölt
számok? Adjuk meg ezeket a számokat is egyetlen kifejezéssel!
c.2) Ebben a sorozatban hányadik helyen áll az 512?
c.3) Melyik szám áll az 529. helyen?
Feladat: 7.3. a) Tudjuk, hogy az
x szám néggyel osztva
1 maradékot
ad. Következik-e ebből, hogy kettővel osztva is
1 a maradék?
b) Tudjuk, hogy az
x szám kettővel osztva
1 maradékot
ad. Következik-e ebből, hogy néggyel osztva is
1 a maradék?
Feladat: 7.4. [
63]
a) Egy szám 10-zel osztva 0 maradékot ad. Mekkora
maradékot ad 5-tel osztva?
b) Egy szám 5-tel osztva 0 maradékot ad. Mekkora
maradékot ad 10-zel osztva?
c) Egy szám 10-zel osztva 1 maradékot ad. Mekkora
maradékot ad 5-tel osztva?
d) Egy szám 5-tel osztva 1 maradékot ad. Mekkora
maradékot ad 10-zel osztva?
e) Egy szám 3-mal osztva 0 maradékot ad. Mekkora
maradékot ad 9-cel osztva?
f) Egy szám 9-cel osztva 0 maradékot ad. Mekkora
maradékot ad 3-mal osztva?
g) Egy szám 3-mal osztva 1 maradékot ad. Mekkora
maradékot ad 9-cel osztva?
h) Egy szám 9-cel osztva 1 maradékot ad. Mekkora
maradékot ad 3-mal osztva?
i) Egy szám 9-cel osztva 2 maradékot ad. Mekkora
maradékot ad 3-mal osztva?
j) Egy szám 3-mal osztva 2 maradékot ad. Mekkora
maradékot ad 9-cel osztva?
Feladat: 7.5. [
108] Igaz-e, hogy ,,bármely" hét egymást követő természetes szám
összege osztható héttel?
Feladat: 7.6. [
63] Próbáljuk meg felbontani a 60-at és a 63-at is két szám összegére
úgy, hogy
a) mindkettő osztható legyen 6-tal;
b) csak az egyik legyen 6-tal osztható!
Feladat: 7.7. [
63] Keressünk két olyan
a) 17-tel nem osztható számot, amelynek az összege
osztható 17-tel;
b) 11-gyel nem osztható számot, amelynek az összege
osztható 11-gyel;
c) számot, amelynek az összege osztható 7-tel! Milyen
esetek lehetségesek?
Feladat: 7.8. [
63] Ebben a feladatban egész számokról van szó. Az alábbi
A,
B
oszlopban levő állításokról tudjuk, hogy igazak. Döntsük el, hogy
a
C oszlopban található állítás biztosan
igaz,
lehet igaz vagy biztosan
hamis. Írjuk a
megfelelő betűt a
C oszlop mellé!
|
A |
B |
C | |
|
x ötös maradéka 2 |
y ötös maradéka 1 |
x+y ötös maradéka 3 | |
|
x+y ötös maradéka 3 |
x ötös maradéka 2 |
y ötös maradéka
1 | |
|
x ötös maradéka 2 |
y ötös maradéka 1 |
x+y tízes
maradéka 3 | |
|
x osztható 7-tel |
y osztható
7-tel |
x+y osztható 7-tel | |
|
x nem osztható 7-tel |
y nem osztható 7-tel |
x+y nem
osztható 7-tel | |
Feladat: 7.9. [
63] Keressünk két olyan számot, amelynek a különbsége
a) osztható 7-tel;
b) osztható
8-cal;
c) osztható 9-cel!
Feladat: 7.10. [
63] Legföljebb hány olyan számot tudsz fölírni, amelyek közül semelyik
kettő különbsége sem osztható 9-cel?
Feladat: 7.11. Pistike nem tud 40-nél nagyobb számokkal számolni. Azt a feladatot
kapta, hogy számolja ki, milyen maradékot ad a
17+38+9+21+35
összeg 3-mal, 4-gyel, 5-tel, 6-tal osztva!
Javasoljunk módszert Pistikének! Fogalmazzunk meg általános
érvényű állítást!
Feladat: 7.12. Ebben a feladatban egész számokról van szó. Az alábbi
A,
B
oszlopban levő állításokról tudjuk, hogy igazak. Döntsük el, hogy
a
C oszlopban található állítás biztosan
igaz,
lehet igaz vagy biztosan
hamis. Írjuk a
megfelelő betűt a
C oszlop mellé!
|
A |
B |
C | |
|
x hármas maradéka 1 |
y hármas maradéka 2 |
x·y hármas maradéka 2 | |
|
x négyes maradéka 2 |
y
négyes maradéka 2 |
x·y négyes maradéka 2 | |
|
x
ötös maradéka 2 |
y ötös maradéka 3 |
x·y ötös maradéka 1 | |
|
x·y hármas maradéka 2 |
y hármas maradéka 2 |
x hármas
maradéka 1 | |
|
x·y négyes maradéka 2 |
y négyes
maradéka 2 |
x négyes maradéka 1 | |
|
x·y ötös maradéka 1 |
y ötös maradéka 3 |
x ötös maradéka
2 | |
Feladat: 7.13. [
63] Fogalmazzuk meg, hogy ha két számot összeszorzunk, a szorzat
osztási maradéka milyen kapcsolatban van a tényezők osztási
maradékával!
Feladat: 7.14. Igaz-e, hogy minden 3-nál nagyobb prímszámnak van 6-tal osztható
szomszédja?
Feladat: 7.15. Bontsuk föl a 190-et négy olyan különböző pozitív egész szám
összegére, amelyek 13-as maradéka azonos!
Feladat: 7.16. Előbb a 100-at, majd a 90-et elosztottuk ugyanazzal a számmal. Az
első esetben 4 volt az osztás maradéka, a másodikban 18. Mi
lehetett az osztó?
Feladat: 7.17. Melyik az a négyjegyű szám, amellyel a 21949-et elosztva 37-et,
25949-et elosztva pedig 53-at kapunk maradékul?
Feladat: 7.18. Egy iskola diákjai azt tapasztalták, hogy akár kettesével, akár
hármasával, akár négyesével, akár ötösével, akár hatosával, akár
hetesével, akár nyolcasával állnak sorba, mindenképpen egy diák
magára marad az utolsó sorban. Hány tanulója van az iskolának, ha
tudjuk, hogy ezernél nincs több?
Feladat: 7.19. Melyik az a legkisebb pozitív egész, amely 3-mal osztva 1-et,
4-gyel osztva 2-t, 5-tel osztva 3-at és 6-tal osztva 4-et ad
maradékul?
Feladat: 7.20. Adjunk meg minél több egész számot úgy, hogy
a) semelyik kettő különbsége se;
b) semelyik kettő összege se;
legyen osztható 5-tel!
Feladat: 7.21. Igaz-e, hogy öt egész szám között mindig van három, amelyek
összege osztható 3-mal?
Feladat: 7.22. Milyen
p prímekre lesz
2p+1,
3p+2,
4p+3 és
6p+1
mindegyike prím?
Feladat: 7.23. Egy
A pozitív egész 3-mal osztva 1 maradékot, 37-tel osztva 33
maradékot ad. Mennyi maradékot ad
A, ha 111-gyel osztjuk?
Feladat: 7.24. Adjunk meg minél több egész számot úgy hogy semelyik
a) kettő különbsége
b)
négyzetének különbsége
se legyen osztható 10-zel!
Feladat: 7.25. Három gyermek -
A,
B és
C - el szeretné dönteni, hogy
melyikük kapja az utolsó darab cukrot.
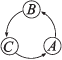
1. ábra
felrajzol egy táblát (lásd
az
1. ábrát) és a következőt
javasolja: ,,Tegyünk egy bábút az
A mezőre, valamelyikünk dobjon
(szabályos) dobókockával és nézzük meg, hogy ha lelépjük a dobott
számot a bábúval, akkor melyikünk mezőjére jut. Legyen azé a
cukorka!"
b)
B módosítást javasol: ,,Így unalmas, vegyük inkább a
dobott szám négyzetét és annyit lépjünk a bábúval
A-ból!"

2. ábra
Közben megjön
D is, ezért
C új táblát rajzol (lásd
a
2. ábrát) és így szól:
,,Játsszunk
ezen a pályán és lépjük le a dobott számot
A-ból indulva!"
d) ,,Szerintem inkább a dobott szám négyzetét lépjük le
itt" - javasolja
D!
A négy sorsolási variáció közül melyek igazságosak és a nem
igazságosak kinek kedveznek?
Feladat: 7.26. Adjunk meg minél több egész számot úgy, hogy
a) semelyik kettő összege és különbsége se;
b) semelyik kettő négyzetének különbsége se
legyen osztható 5-tel!
Feladat: 7.27. Milyen számjegyre végződik
21997
?
Feladat: 7.28. Határozzuk meg
20022005
+
20092005
utolsó számjegyét
Feladat: 7.29. A
2,
22
,
23
,… sorozatban található-e két olyan
különböző szám, amelyek különbsége osztható 100-zal?
Feladat: 7.30. Osztható-e 100-zal a
7+
72
+
73
+
74
+…+
718
+
719
+
720
összeg?
Feladat: 7.31. [
63] Van-e a következő sorozatokban négyzetszám?
a)
2,6,10,14,18,22,26,30,…
b)
11,21,31,41,51,61,…
c)
12,22,32,42,52,62,…
Feladat: 7.32. Vizsgáljuk meg az
1,
14,
144,
1444,
14444,
…
számokat! Közülük melyek négyzetszámok?
Feladat: 7.33. [
63] Milyen
x és
y pozitív egész számok lehetnek megoldásai a
következő egyenletnek?
a)
x2
=4y+1 b)
x2
=4y+2 c)
x2
=4y+3
Feladat: 7.34. [
63] Milyen maradékot adhatnak 8-cal osztva a
négyzetszámok?
Feladat: 7.35. [
63] Milyen
p prímszámra lehet a
p2
+8 prímszám?
Feladat: 7.36. [
63]
2100
milyen maradékot ad 10-zel osztva?
Feladat: 7.37. [
63]
3100
milyen maradékot ad 7-tel osztva?
Feladat: 7.38. [
63] Mi a maradék, ha
21988
-at elosztjuk 7-tel?
A
2n
szám 7-tel való osztási maradéka
n melyik
tulajdonságától függ?
Feladat: 7.39. [
63]
a) Határozzuk meg a
3207
hatvány 5-tel való osztási
maradékát!
b) Mitől függ a
3n
hatvány 5-tel való osztási
maradéka?
Feladat: 7.40. Bizonyítsuk be, hogy
a)
1020
+8 osztható
72-vel!
b)
1033
+8 osztható 9-cel!
c)
1010
+14 osztható 6-tal!
Feladat: 7.41. [
63] Bizonyítsuk be, hogy ha
n természetes szám, akkor
3
n2
+2n+1
nem osztható 5-tel!
Feladat: 7.42. Lehet-e négy egymást követő pozitív egész összege
négyzetszám?
Feladat: 7.43. [
63] Bizonyítsuk be, hogy ha
x pozitív egész szám, akkor
a)
5∣
x5
-x;
b)
30∣
x5
-x;
Feladat: 7.44. Készítsünk algoritmust, ami az osztás művelete nélkül megvalósítja
a) a
mod
b) a
divfunkciót.