2. FEJEZET: Osztók
Feladat: 2.1. [
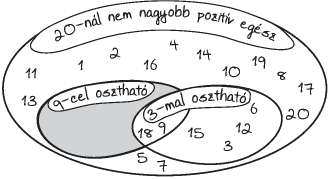
63] Az első húsz pozitív egész számot osztályoztuk
az
1. ábrán. A szürkével színezett részbe
egyetlen szám sem került. Ez érthető is, mert nincs olyan szám,
amely 9-cel osztható, de 3-mal nem.
1. ábra
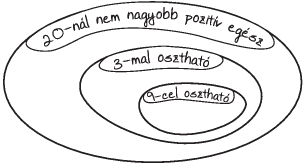
A 9-cel osztható számok a 3-mal oszthatók közül valók. Ezt a
kapcsolatot jól kiemeli a
2. ábra. Írjuk be ide
is az első húsz pozitív egész számot!
2. ábra
Feladat: 2.2. Rajzoljunk számegyenest és jelöljük be rajta az egész számokat
0-tól 30-ig! Jelöljünk meg minden hárommal osztható számot nagy
piros karikával, minden néggyel oszthatót kis tömör kék körrel, a
néggyel nem osztható párosakat kis zöld tömör körrel.
Feladat: 2.3. [
63] Írjuk be az
1. ábra megfelelő helyeire az 1, 2,
3, 4, 5, 6, 8, 12, 16, 21, 24, 30, 36 számokat! Maradt-e rész
üresen? Van-e olyan egész szám, amelynek ott lenne a helye?
1. ábra
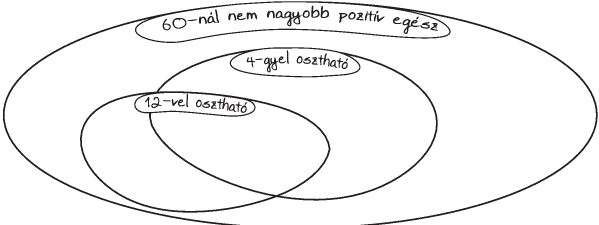
Feladat: 2.4. [
63] A rajzok címkéiről hiányzik a felirat.
El lehet-e helyezni az
1. ábrán a címkékre a
,,12-vel osztható", ,,4-gyel osztható" feliratokat úgy, hogy
minden 60-nál nem nagyobb pozitív egész számot be lehessen írni
valahova?

1. ábra
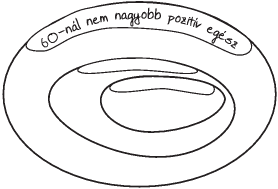
Feladat: 2.5. [
63] Az
1. és a
2. ábrán is a
,,12-vel osztható", ,,10-zel osztható" kifejezéseket kell a
címkékre írni.
Csak az egyik ábrába lehet beírni az összes 60-nál nem nagyobb
pozitív egész számot. Írjuk is be őket!
A másik ábrába milyen tulajdonságú számokat nem lehet elhelyezni?
1. ábra
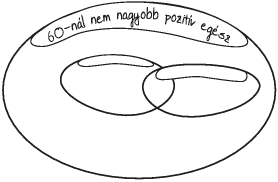
2. ábra
Feladat: 2.6. [
63] Ábrázoljuk egy halmazábrán a 60-nál nem nagyobb pozitív egész
számok közt
a) a 12-vel osztható számokat és a 8-cal osztható
számokat;
b) az 5-tel osztható számokat és a 15-tel osztható
számokat!
Feladat: 2.7. [
63] Színezzük be az
1. ábrának azokat a részeit,
ahova egy szám sem kerülhet! Az ábra többi részeibe írjunk
számokat!
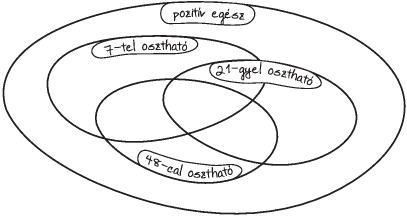
1. ábra
Lehet-e itt is olyan ábrát rajzolni, ahol egy rész sem marad
üresen?
Feladat: 2.8. [
63] Helyezzünk el 3-3 pozitív egész számot
az
1-
4. halmazábrák egyes
részeibe, ahová lehet! Színezzük be az üresen maradó részeket!
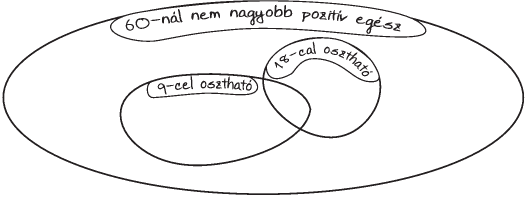
1. ábra
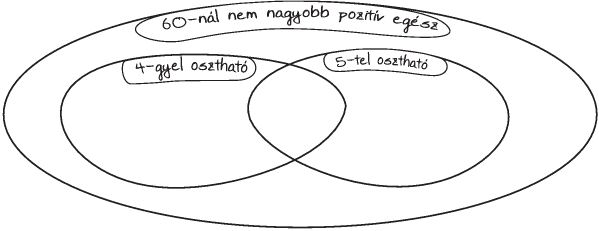
2. ábra
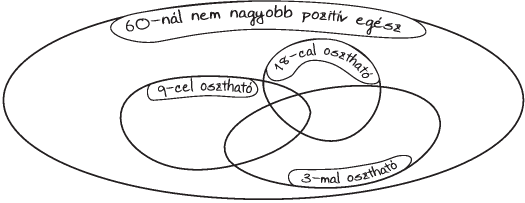
3. ábra
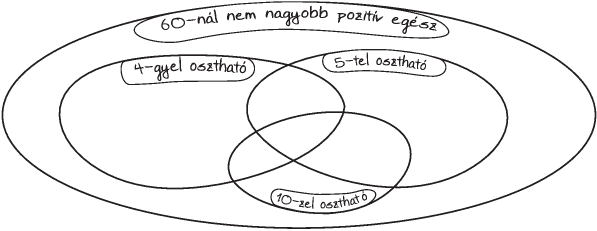
4. ábra
Feladat: 2.9. [
63] Címkézzük meg a halmazábrákat a megadott feliratokkal!
1. ábra: 5-tel osztható 10-zel
osztható 20-szal osztható
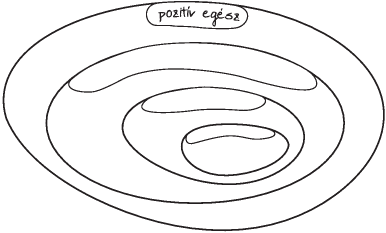
1. ábra
. ábra: 2-vel osztható 3-mal
osztható 12-vel osztható
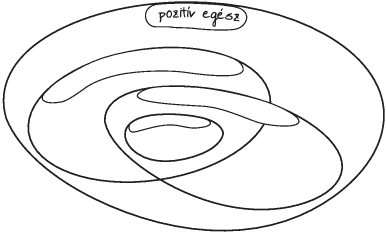
2. ábra
. ábra: 2-vel osztható 3-mal
osztható 5-tel osztható
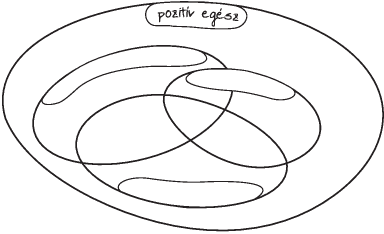
3. ábra
. ábra: 3-mal osztható 5-tel
osztható 6-tal osztható
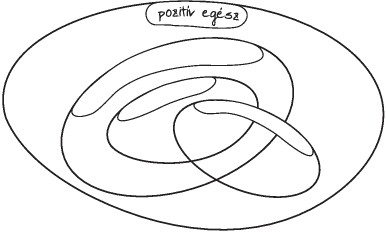
4. ábra
Feladat: 2.10. [
63] Párosítsuk az alábbi címkehármasokat
az
1-
3. ábrákkal! Címkézzük
is meg az ábrákat, és írjunk mindegyik részbe néhány számot!
a) 4-gyel osztható 12-vel osztható 60-nal
osztható
b) 4-gyel osztható 11-gyel osztható 12-vel
osztható
c) 4-gyel osztható 11-gyel osztható 13-mal
osztható
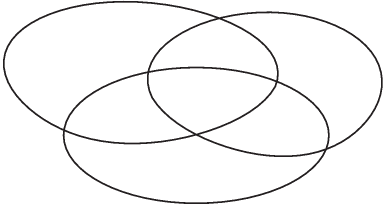
1. ábra

2. ábra
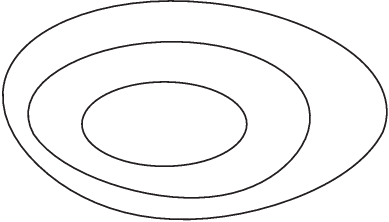
3. ábra
Feladat: 2.11. [
63] Színezzük be az
1-
3 ábrák
üresen maradó részeit! Készítsünk olyan ,,gazdaságos" ábrákat,
ahol egy rész sem marad üresen!
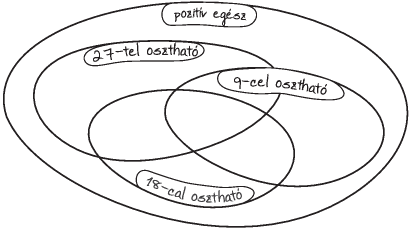
1. ábra
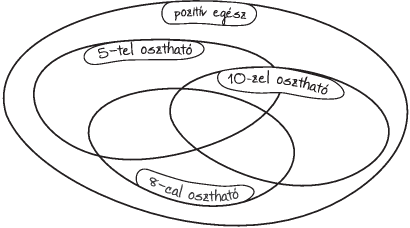
2. ábra
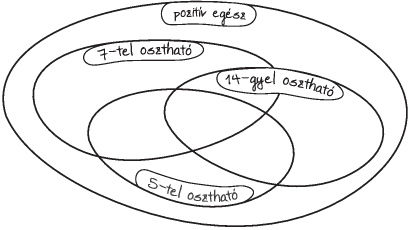
3. ábra
Feladat: 2.12. [
63] Színezzük be az
1-
3 ábrák
üresen maradó részeit! Készítsünk olyan ,,gazdaságos" ábrákat,
ahol egy rész sem marad üresen!
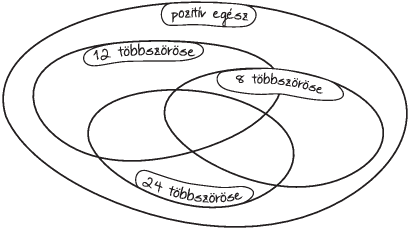
1. ábra
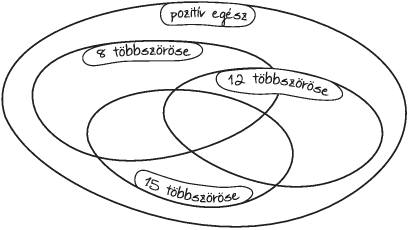
2. ábra
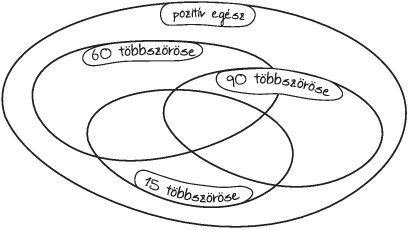
3. ábra
Feladat: 2.13. Milyen oszthatósági feltétellel megadott halmazok láthatók
az
1 ábrán látható két
,,gazdaságos" Venn-diagrammon?
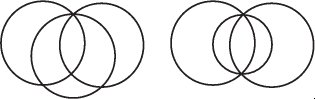
1. ábra
Feladat: 2.14. [
63] Igazak-e a következő állítások? Írjunk az
igazak mellé
i betűt, a
nem igazak mellé
n betűt!
(1) A 3-mal osztható számok mind oszthatók 6-tal.
(2) A 6-tal osztható számok mind oszthatók 3-mal.
(3) Van olyan 6-tal osztható szám, amelyik osztható
3-mal.
(4) Van olyan 3-mal osztható szám, amelyik osztható
6-tal.
(5) Van olyan 6-tal osztható szám, amelyik nem osztható
3-mal.
(6) Van olyan 3-mal osztható szám, amelyik nem osztható
6-tal.
(7) Van olyan 3-mal osztható szám, amelyik páratlan.
(8) Van olyan 6-tal osztható szám, amelyik páratlan.
(9) Minden 3-mal osztható szám páros.
(10) Minden 6-tal osztható szám páros.
(11) Minden 6-tal osztható szám jegyeinek az összege
osztható 3-mal.
(12) Nincs olyan 6-tal osztható szám, amely jegyeinek
összege ne lenne osztható 3-mal.
(13) Minden 6-tal osztható szám jegyeinek az összege
osztható 6-tal.
(14) Van olyan négyzetszám, amely 3-mal osztható, de
9-cel nem.
(15) Nincs olyan négyzetszám, amely 3-mal osztható, de
9-cel nem.
(16) Minden 3-mal osztható négyzetszám 9-cel is osztható.
Feladat: 2.15. Tegyük fel, hogy
x olyan szám, amelyre az alábbi hat állítás
közül pontosan három teljesül:
a) páros;
b) osztható 3-mal;
c) osztható 12-vel;
d) osztható 15-tel;
e) osztható 30-cal;
f)
osztható 60-nal.
Meg lehet-e teljes bizonyossággal állapítani, hogy melyik az a 3
állítás, amelyik nem igaz
x-re?
Feladat: 2.16. Készítsünk algoritmust, ami beolvas két számot és eldönti, hogy az
egyik osztója-e a másiknak!
Feladat: 2.17. Készítsünk algoritmust, ami kiválogatja egy vektorból a hárommal
osztható számokat!
Feladat: 2.18. Készítsünk algoritmust, ami megszámolja egy vektorban az adott
(beolvasott) számmal osztható számokat.


























