21. FEJEZET: Vegyes feladatok
Feladat: 21.1. Melyek azok a háromjegyű prímszámok, amelyek számjegyeit
összeszorozva 10-et kapunk?
Feladat: 21.2. [
108] Egy urnában 67 fehér és piros golyó van. Vannak köztük kicsik és
nagyok. Tudjuk :
-a piros golyók száma osztható 5-tel;
-a nagy piros golyók száma egyenlő a fehér
golyókéval;
-a legkevesebb a kis fehér golyókból van;
-mindegyik fajta golyó száma prím.
Hány golyó van az egyes fajtákból?
Feladat: 21.3. [
108] Oldjuk meg a prímek körében a
egyenletet!
Feladat: 21.4. Vágjunk ki kartonból szabályos sokszöget, középpontját rögzítsük
gombostű hegyével, és forgassuk e körül. Határozzuk meg azt a
legkevesebb oldalszámú sokszöget, amelyik
25,
5∘
-os
elforgatás után egybeesik eredeti kontúrjával.
Feladat: 21.5. [
36] 7800 Ft-ot fizettem ki 1000-es, 500-as és 100-as címletű
bankjegyekben. Az 500-as és a 100-as bankjegyek száma megegyezett.
Hány db bankjeggyel fizethettem?
Feladat: 21.6. [
36] Két természetes szám összege 13574. Az egyik szám 10-zel osztható.
Ha ennek utolsó jegyét elhagyom, akkor éppen a másik számot kapom.
Melyik ez a két szám?
Feladat: 21.7. [
36] Hány olyan - egymással nem egybevágó - háromszög létezik,
amelynek két oldala 21 és 27 cm, harmadik oldala - cm-ben mérve
- hárommal osztható szám, kerületének mért mérőszáma pedig héttel osztható?
Mekkora a harmadik oldal?
Feladat: 21.8. [
108] Egy baráti társaság elment kirándulni. A nagy erdei tisztáson a
következő játékot találták ki: körbeálltak, Jolán kezdte a játékot
úgy, hogy először mindenki a baloldali szomszédjának dobta a
labdát, majd miután Jolánhoz visszajutott a labda, mindenki a
baloldali második szomszédjának dobta, amíg az ismét Jolánhoz nem
került. És így tovább. A játékból kiesik az, aki valamelyik
fordulóban nem jut labdához, mielőtt az visszakerülne Jolánhoz.
Kevesebben voltak 20-nál. Hányan lehettek, ha tudjuk, hogy a
játékból senki sem esett ki?
Feladat: 21.9. [
108] Melyik az a legkisebb prímszám, amelyet elő lehet állítani 2, 3, 4
és 5 különböző prímszám összegeként is?
Feladat: 21.10. [
108] Mely
p és
q prímekre lesz
pq-1 és
pq+1 is prím?
Feladat: 21.11. Egy dobozban 103 kavics van. Péter és Pál felváltva vesznek ki a
dobozból legalább egy, de legfeljebb 10 kavicsot. Amikor a doboz
kiürült, mindketten megszámolják, hogy összesen hány kavicsot
vettek ki külön-külön. Ha ez a két szám relatív prím, akkor Péter
nyert. A játékot kezdő Péter tud-e úgy játszani, hogy biztosan ő
nyerjen?
Feladat: 21.12. Bontsuk fel két háromjegyű szám szorzatára az 555555-öt és a
777777-et!
Feladat: 21.13. [
98] Varázsországban a Nagy Zöld Sárkánynak 100 feje van. A mesebeli
Vitéznek olyan kardja van, amivel egy csapásra csak 33 vagy 21
vagy 17 fejét tudja levágni. Igen ám, de az első esetben a
Sárkánynak 18 új feje nő ki, a második esetben 36, a harmadikban
pedig 14. Ha a Sárkánynak az összes feje lehullott, akkor már nem
nő ki több. Le tudja-e győzni a Vitéz a Sárkányt?
Feladat: 21.14. [
108] Egy
10×10-es négyzetalakú táblázatba beírjuk az egész
számokat 1-től 100-ig úgy, hogy az első sorba 1-től 10-ig, a
másodikba 11-től 20-ig, stb növekvő sorrendbe írjuk le a számokat.
Bizonyítsuk be, hogy akárhogyan is veszünk ki ebből a táblázatból
egy 7-szer 7-es összefüggő résztáblázatot, az ebben leírt számok
összege mindig osztható 49-cel!
Feladat: 21.15. [
108] Egy
10×10-es négyzetalakú táblázatba beírjuk az egész
számokat 0-tól 99-ig úgy, hogy az első sorba 0-tól 9-ig, a
másodikba 10-től 19-ig, stb növekvő sorrendbe írjuk le a számokat.
Ezután elhelyezünk a táblázaton 10 db korongot úgy, hogy a sakk
szabályai szerint mint bástyák ne üssék egymást. Adjuk össze az
általuk lefedett számokat és bizonyítsuk be, hogy bármely, a
feltételeknek megfelelő lefedés esetén ez az összeg osztható 5-tel
és 9-cel is!
Feladat: 21.16. [
63]
a) Egy szultán börtönének 100 cellájában 100 elítélt
raboskodott. Mindegyik ajtaján egy-egy kétállású zár volt, amely
egy forgatásra nyithatóvá tette az ajtót, de még egy forgatásra
zárt. Egyik nap a szultán jókedvében leküldte a börtönbe első
szolgáját, hogy fordítson minden cella zárján egyet. Hamar gondolt
egy újat és leküldte második szolgáját is, hogy az minden második
záron forgasson még egyet. Iziben küldte is harmadik szolgáját,
hogy az minden harmadik záron fordítson. Ez így ment a 100-adik
szolgáig, aki csak a legutolsó, a 100-adik záron fordított egyet.
Mely ajtók mögül szabadulhatott ki a rab ezek után?
b) A szultánnak az a parancsa, hogy az első őr minden
záron fordítson egyet, a második őr minden második záron fordítson
kettőt, a harmadik minden harmadikon hármat, és így tovább, és
végül a századik minden századikon százat. Mely cellák lakói
hagyhatják el a börtönt?
Feladat: 21.17. Egy számnak 100 osztója van. Mi lesz az eredmény, ha
összeszorozzuk a száz osztót?
Feladat: 21.18. [
39] Egy pozitív egész összes (pozitív) osztójának összegét elosztjuk
ugyanezen osztók reciprokainak összegével. Mit kapunk eredményül?
Feladat: 21.19. Összeszorozzuk 1-től kezdve az első 100 pozitív egész
számot:
|
1·2·3·4·5· … ·97·98·99·100
|
Mi az utolsó
0-tól különböző számjegye az így kapott számnak?
Feladat: 21.20. Írjunk egy
3×3-as táblázat 9 mezőjébe 9 különböző pozitív
egész számot úgy, hogy minden sorban és minden oszlopban a számok
szorzata 270 legyen!
Feladat: 21.21. Egy hajóskapitánynak fia is van lánya is van. Életkorának, a hajó
méterben mért hosszának és gyerekei számának szorzata 32118. Hány
éves a kapitány?
Feladat: 21.22. A görögök
tökéletes számnak nevezték azokat a számokat,
amelyek egyenlők önmaguknál kisebb osztóik összegével. A legkisebb
pozitív tökéletes szám a
6, hiszen
6=1+2+3. Melyek a
100-nál kisebb tökéletes számok?
[Ajánlott olvasmányok:
[151] 1. fejezete, [16] ,,Püthagoreusok
számelmélete" című fejezete (86-87. oldal)]
Feladat: 21.23. Hány olyan 1000-nél nem nagyobb pozitív egész szám van, amely a
a) 2 és 3 számok közül pontosan eggyel;
b) 2, 3 és 5 számok közül pontosan eggyel osztható?
Feladat: 21.24. [
63] Igaz-e, hogy öt egymást követő természetes szám szorzata osztható
8-cal? 16-tal? 24-gyel? 5-tel? Mi a legnagyobb szám, amellyel
biztosan osztható?
Feladat: 21.25. [
63] Igaz-e, hogy ha öt pozitív egész szám szorzata két nullára
végződik, akkor van köztük olyan négy szám, melyeknek a szorzata
is két nullára végződik?
Feladat: 21.26. A tanár egy nagy pozitív egész számot írt a táblára. A diákok a
számot látva így szóltak:
1. tanuló: a táblára írt szám osztható 2-vel;
2. tanuló: a szám 3-mal is osztható;
3. tanuló: 4-gyel is ....; és ez így ment tovább az utolsó (30.)
tanulóig:
30. tanuló: ez a szám 31-gyel is osztható.
A tanár pedig így válaszolt: két diák kivételével mindenkinek
igaza van. Ez a két diák pedig egymás után szólalt meg.
Melyik két diák tévedett?
Feladat: 21.27. Hét gazfickó a sötét erdő mélyén megbúvó kunyhóban sajátos módon
osztozkodott a rabolt aranyakon. Körbe ültek és egyikőjük
megszámolta a zsákmányolt aranytallérokat. Nosza, el is vett
magának annyit, amennyi a tallérok száma számjegyeinek összege.
Erre biza' jobboldali szomszédja is nekiállt megolvasni a maradék
aranyakat és ő is épp annyit tett el magának, mint az
aranytallérok száma számjegyeinek összege. Így ment ez sorban, két
körön át, mígnem elfogyott az utolsó aranytallér is. Csudálkoztak
is fenemód, hogy nem ám csak mindőjük éppen kétszer vett, de
egyformán is jutott mindegyik gonosznak, csupáncsak hírhedett
vezérük Sobri Jóska lett náluknál gazdagabb.
Hányadiknak vett Sobri Jóska az aranyból?
Feladat: 21.28.
104
-nek legfeljebb hány pozitív osztója adható meg úgy, hogy
egyik se legyen osztója valamelyik másiknak?
Feladat: 21.29. Számozzuk meg sorrendben egy
8×8-as sakktábla sorait és
oszlopait, és minden mezőre írjuk rá a mező sorszámának és
oszlopszámának összegét. Helyezzünk most el 8 bástyát a táblán
úgy, hogy semelyik kettő se üsse egymást, azaz minden sorban és
minden oszlopban pontosan egy bástya álljon. Melyik
bábuelhelyezésnél lesz a bástyák alatti számok összege a lehető
legnagyobb?
Feladat: 21.30. Oldjuk meg az alábbi egyenletet a természetes számok körében:
Feladat: 21.31. Tudjuk, hogy
|
3·8·15·24·35·…·899
4·9·16·25·36·…·900
=
p
q
,
|
ahol
p,q>0 egészek és
(p,q)=1. Számítsuk ki
p és
q értékét (a bal oldali tört
nevezőjében a négyzetszámok szorzata szerepel 4-től 900-ig, a
számlálóban a megfelelő tényezők pedig az 1-gyel kisebb számok)!
Feladat: 21.32. Adott egy
19∘
-os szög. Csak körző és vonalzó
felhasználásával szerkesszünk ennek alapján
1∘
-os szöget!
(Leírandó a szerkesztés menete!)
Feladat: 21.33. Képeztük egy háromjegyű szám és fordítottjának különbségét.A
kapott szám első jegye 3.
a) Mennyi a különbség?
b) Mik lehettek az eredeti számok?
Feladat: 21.34. [
63] Van-e olyan négyzetszám, amelyben a számjegyek összege
a) 150;
b) 18?
Feladat: 21.35. [
63] Igaz-e, hogy ha
x egész szám, és
x2
osztható 6-tal, akkor
x
is osztható 6-tal?
Feladat: 21.36. [
63] Keressünk olyan négyzetszámot, amelynek a számjegyeit összeadva az
eredmény
a) 21;
b) 15;
c) 27;
d) 36;
e) 8!
Feladat: 21.37. [
63] Milyen maradékot adhat egy négyzetszám jegyeinek az összege
a) 3-mal osztva;
b) 9-cel osztva?
Feladat: 21.38. [
63] Bizonyítsuk be, hogy ha
p és
p2
+8 törzsszámok, akkor
p2
+p+1 is törzsszám!
Feladat: 21.39. [
63] Van-e olyan pozitív egész
n, amelyre
17∣
11n
?
Feladat: 21.40. [
63] Van-e egész megoldása a következő egyenletnek?
a)
x2
=3y+2
b)
x2
=3y+1
c)
x2
+
y2
=4z+3
d)
x2
+
y2
+
z2
=8k+7
Feladat: 21.41. [
63] A 8 és a 9 két olyan egymást követő szám, melyek mindegyike
hatványszám, vagyis egy egész számnak 1-nél nagyobb kitevőjű
hatványa (
8=
23
,
9=
32
). Nehéznek látszó megoldatlan
probléma a matematikában, hogy van-e még a számsorban valahol
egymás mellett két hatványszám. Az is megoldatlan, hogy van-e a
számsorban valahol három egymást követő hatványszám. Próbáljuk
meggondolni, hogy van-e a számsorban négy egymást követő
hatványszám!
Feladat: 21.42. [
63] Írjunk a 423-hoz három számjegyet úgy, hogy az így keletkezett
hatjegyű szám osztható legyen 5-tel, 6-tal és 7-tel!
Feladat: 21.43. [
63] Mi lehet az utolsó négy jegye egy 25-re végződő szám
négyzetének?
Feladat: 21.44. [
63] Igaz-e, hogy a következő sorozatban végtelen sok 3-mal osztható
szám van? Bizonyítsuk is állításunkat!
|
5, 55, 555, 5555, 55 555,…
|
(a sorozat
n-edik eleme olyan
n jegyű szám, amelynek minden
számjegye 5).
Feladat: 21.45. [
63] Igaz-e, hogy a
|
31, 331, 3331, 33 331, 333 331,…
|
sorozatban (a sorozat
n-edik eleme olyan
(n+1) jegyű szám,
amelynek az első
n számjegye 3, az utolsó számjegye pedig 1)
a) végtelen sok 13-mal osztható szám van;
b) végtelen sok 7-tel osztható szám van?
Igazoljuk is az állítást!
Feladat: 21.46. [
63] Bizonyítsuk be, hogy a következő számtani sorozatban végtelen sok
csupa 2-es számjegyből álló szám van! (A számtani sorozat egymást
követő elemei között a különbség állandó.)
Feladat: 21.47. Ebben a feladatban az
összeget vizsgáljuk. Mutassuk meg, hogy az összeg értéke nem lehet
egész szám, ha
a)
n=1024
b)
n=1021
c)
n=1000.
d Van-e olyan 1-nél nagyobb
n egész szám, amelyre a
vizsgált összeg értéke is egész?
Feladat: 21.48. Az
a1
,
a2
,
a3
,
…,
a49
pozitív egész számok
összege 999. Legfeljebb mennyi lehet ennek a 49 számnak a
legnagyobb közös osztója?
Feladat: 21.49. Legfeljebb hány számot lehet kiválasztani az
1,
2,
3,
…,
100 számok közül úgy, hogy
a) bármelyik kettő relatív prím legyen?
a) egyik se legyen osztója másik kiválasztottnak?
Feladat: 21.50. [
117] András a tengerparton kagylót gyűjtött. Hat csoportba rendezte
fajtájuk szerint. - Érdekes - mondta, a különböző kupacokban
lévő kagylók száma páronként relatív prím. Ezután két kupacot
kiválasztott, mindkettőből elvett egy-egy kagylót, s ezeket a
vödrébe tette. Összesen kilencszer választott kupacpárt, s vett el
egy-egy kagylót. Így a hat kupacban ugyanannyi kagyló maradt. Hány
kagylót gyűjtött Andris és hogyan csoportosította azokat?
Feladat: 21.51. Írjunk be az alábbi táblázat 6 mezőjébe egy-egy 0-tól különböző
számjegyet úgy, hogy a két sorban (balról jobbra) egy-egy pozitív
egész szám négyzete álljon, továbbá a három oszlopban is
négyzetszámok legyenek!
Feladat: 21.52. Oldjuk meg a következő rejtvényt:
Azonos betűk azonos, különböző betűk
különböző számjegyeket jelölnek.
Feladat: 21.53. Határozzuk meg azokat a négyjegyű, 9-re végződő számokat, amelyek
oszthatók számjegyeik mindegyikével.
Feladat: 21.54. Nehezített számlétra
Két játékos felváltva mond pozitív egész számokat. A kezdőnek 1-et
kell mondania, az
n-edszerre megszólaló játékos pedig az
ellenfele által legutóbb kimondott számot valamely 1 és
n
közötti egész számmal növelheti meg. Az nyer, aki kimondja a
100-at.
Kinek van nyerő stratégiája?
Feladat: 21.55. [
108] Mi lesz a végeredményül kapott tört nevezője
100!
2100
egyszerűsítése után?
Feladat: 21.56. [
40] Bergengóciában pénzreformot vezettek be. Ezentúl csak ötbengócos
és hétbengócos
[bengóc a bergengóc forint] lesz.
a) Lehet-e 101 bengóc egy csoki ára? Azaz ki lehet-e
fizetni pontosan 101 bengócot, ha nem tudnak visszaadni?
b) Mely összegek fizethetők ki visszaadás nélkül?
c) És visszaadással?
Feladat: 21.57. [
40] Bergengócia új uralkodója saját képét
szeretné a bengócokon viszontlátni. Ezért a
régi pénzeket visszavonja, ezentúl csak
6 és
15 bengócosok lesznek. Most mit lehet kifizetni
a) visszaadással;
b) visszaadás nélkül?
Feladat: 21.58. [
36] A 948 és a 417 minegyikét ugyanazzal a kétjegyű számmal elosztva
egyenlő maradékokat kapunk. Mekkora a maradék?
Feladat: 21.59. [
40] Melyik az az
n pozitív egész szám, amelyre a
23479 szám
n-nel osztva
50-nel nagyobb maradékot ad, mint a
34539?
Feladat: 21.60. [
40] Számítsuk ki az
11111111 és a
100 darab
1-esből álló szám
legnagyobb közös osztóját!
Feladat: 21.61. [
40] Adjuk meg az összes olyan
n egész számot, amelyre a
7n+6
5n+3
tört tovább egyszerűsíthető!
Feladat: 21.62. [
65] Milyen
k természetes számokra lesznek a következő törtek
természetes számok?
a)
3k-1
5
b)
22k+12
7
c)
16k+12
5
d)
k+11
k-9
e)
k+17
k-3
f)
k+17
k-6
Hány megfelelő
k érték található az egyes feladatokban? Ahol
végtelen sok, ott írjuk fel az általános alakjukat is!
Feladat: 21.63. [
108] Adjuk meg az összes olyan
n egész számot, amelyre a
a)
n+3
n-3
;
b)
n2
+2
n+1
tört értéke egész szám!
Feladat: 21.64. [
63] Egy téglalap alakú lap egyik oldala 385 cm, a másik 105 cm.
Egységoldalú négyzetekre fel lehet darabolni maradék nélkül, 2
egység oldalúakra nem lehet feldarabolni maradék nélkül. Lehet-e
3, 4, 5, 6, 7, 8, 9, 10, 11,
… egység oldalú négyzetekre
maradék nélkül feldarabolni?
Mekkora a legnagyobb olyan négyzet oldala, amilyenre fel lehet
darabolni maradék nélkül?
Feladat: 21.65. [
63]

1. ábra
Egy 30 cm
× 84 cm-es téglalap alakú papírlapnak behajtjuk
a sarkát az
1. ábrán látható módon és
30 cm oldalú négyzeteket hajtogatunk belőle, amennyit csak lehet.
A négyzeteket levágjuk, és a megmaradó csíkból olyan négyzeteket
hajtogatunk, amelyeknek az oldala a papírcsík kisebbik oldalával
egyezik meg (esetünkben 24-gyel). Ebből is annyit hajtogatunk,
amennyit csak tudunk (példánkban egy 24 cm oldalú négyzetet
tudunk,
2. ábra).
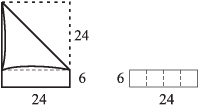
2. ábra
A négyzetet levágjuk, és a megmaradó csíkból hasonló módon mindig
négyzeteket hajtogatunk, egészen addig, amíg sikerül a papírcsíkot
csupa négyzetre hajtogatni.
Csináljuk meg az alábbi méretű téglalapokra is!
a)
16×36
b)
50×36
c)
51×36
Feladat: 21.66. [
40] Beszínezzük a koordinátarendszer rácspontjait. Egyetlen szabályt
kell betartanunk: az
(a;b) pontnak ugyanolyan színűnek kell
lennie, mint az
(a-b;a) és az
(a;b-a) pontnak, bármely egész
számokat jelöljön is
a és
b. Következik-e a szabályból, hogy
a) a
(19;99) és a
(199;3383) pontok;
b) a
(234;1001) és a
(611;7007) pontok
egyforma színűek lesznek?
Feladat: 21.67. [
117] Az
n×m-es sakktábla egy fehér sarkából indul a futó. A
tábla széléhez érve mindig elfordul derékszögben (lásd
az
1. ábrát!), ha sarokba ér
megáll.
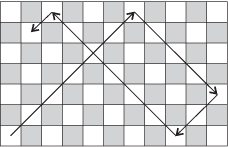
1. ábra
Mely
n és
m esetén járja be a futó az összes fehér
mezőt?
b) Összesen hány mezőt érint az
n×m-es
sakktáblán?
Feladat: 21.68. [
117] Felírtuk az
n=135 és a
k=311 számokat. Ketten játszanak,
felváltva átírják
n és
k értékét.
A soron lévő játékos
n és
k közül kiválasztja a nagyobbikat, s
néhányszor levonja belőle a kisebbiket. (Legalább egyszer le kell
vonnia a kisebbik számot, de a kivonás eredménye soha nem lehet
negatív.) Ezután a kisebbik számot és az új számot írja
n és
k
helyébe és átadja a stafétabotot a másik játékosnak.
Kinek van nyerő stratégiája, ,,Kezdő"-nek, vagy ,,Második"-nak,
ha az
a) nyer;
b) veszít
aki már nem tud változtatni a számokon?
Feladat: 21.69. [
75,
16] Alább egy ókori egyiptomi algoritmikus számolási eljárás egy
példája látható mai számírással átírva. A számolás a 41, 37
számokból indul ki. Mire való az eljárás és hogyan működik?
Magyarázzuk meg!
| | 4 | 1 | 3 | 7 |
| | 8 | 2 | 1 | 8 |
| 1 | 6 | 4 | | 9 |
| 3 | 2 | 8 | | 4 |
| 6 | 5 | 6 | | 2 |
| 1 | 3 | 1 | 2 | | 1 |
| 1 | 5 | 1 | 7 | | |
Feladat: 21.70. [
39] II. Pomádé király halálosan gyűlölte elődjét, I. Pomádét, ezért
országában betiltotta az 1-es számjegy használatát. Országában így
kellett számolni:
|
2, 3, 4, 5, 6, 7, 8, 9, 20, 22, … .
|
Vajon
milyen számot használtak II. Pomádé király birodalmában az 1998
helyett? Más szóval, melyik az 1998. szám a számsorukban?
Feladat: 21.71. Lisztet árulunk. Van egy kétkarú mérlegünk, amellyel
a) 1-től 10-ig
b) 1-től 32-ig
kezdve minden egész kilogrammnyi tömeget ki szeretnénk mérni.
Ehhez kiválaszthatunk néhány mérősúlyt. Legkevesebb hány
mérősúllyal odható meg a feladat? Hány kg-osak legyenek a
mérősúlyok?
c) Öt ügyesen választott mérősúllyal hány kg-ig tudunk
minden egész kilogrammnyi tömeget kimérni?
Feladat: 21.72. Az asztalon van egy kő, melynek tömegéről tudjuk, hogy
kilogrammban mérve egész és legfeljebb
a) 10 kg
b) 32 kg.
Egy kétkarú mérleg és néhány ügyesen megválasztott mérősúly
segítségével kell eldöntenünk, hogy pontosan mennyi a kő tömege.
Legkevesebb hány mérősúllyal odható meg a feladat? Hány kg-osak
legyenek a mérősúlyok? (A mérleget többször is használhatjuk.)
c) Határozzuk meg az
n egész szám legnagyobb értékét
úgy, hogy öt megfelelő segédsúly és egy kétkarú mérleg
segítségével, bármely olyan kő tömege meghatározható legyen,
amelyről tudvalevő, hogy tömegének kilogrammban vett mérőszáma
1
és
n közti egész szám! (A kétkarú mérleget tetszőleges sokszor
használhatjuk, de csak a segédsúlyokat és mérendő tárgyat
rakhatjuk serpenyőibe, és ezeket nem darabolhatjuk fel.)
Feladat: 21.73. [
58] Az alábbi - kissé hiányos - táblázat megmutatja, hogyan
számolnak a heva törzsbeliek saját nyelvükön és melyik
testrészükre mutatva jelzik az adott számot.
| namalu | 2 | bal mutatóujj |
| keli | 5 | bal kisujj |
| tagu | 7 | |
| aluene | 8 | bal könyök |
| kolu | | |
| opey | 12 | bal fül |
| 1 | |
| aley | 10 | |
| ilaw | 11 | a nyak bal része |
| favalo | 3 | bal kéz középső ujj |
| kay-maluene | 22 | jobb csukló |
| | jobb kéz a csukló és a könyök között |
| ni | | bal szem |
| kay-tamey | 19 | |
| 24 | jobb mutatóujj |
| 6 | |
| kay-name | 23 | |
| kay-kolu | 26 | |
| kay-keli | | |
| patapa | | orr |
Töltsük ki a táblázat hiányosságait!
Feladat: 21.74. Alább két szomszédos páros egész szám négyzetét láthatod.
|
152415787751564791571470221617965857842778256
|
|
152415787751564791571519604333606302695344324
|
Határozzuk meg a közöttük található páratlan szám négyzetét!
Feladat: 21.75. Bizonyítsuk be, hogy
5n
bármely
n>0 egész esetén előáll két
pozitív négyzetszám összegeként!
Feladat: 21.76. [
32] Volt egyszer két testvér, s kettejüknek volt egy birkanyája.
Fogták magukat, eladták a birkákat, s pontosan annyi rubelt kaptak
minden egyes birkáért, ahány birka összesen volt a birkanyájban. A
kapott pénzt a következőképpen osztották el: először az idősebb
testvér vett el magának 10 rubelt, majd az öccse, aztán megint az
idősebb fiú, és így tovább. Utoljára a fiatalabbnak már nem jutott
10 rubel, ezért elvette az aprópénzt, s hogy igazságos legyen az
osztozkodás, az idősebbik nekiadta még a bicskáját. Mennyit ért a
bicska?
Feladat: 21.77. Tekintsük az
|
n=1234567891011…200020001
|
számot!
a) Négyzetszám-e az
n szám?
b) Az
n szám jegyeinek felcserélésével kaphatunk-e
négyzetszámot?
Feladat: 21.78. Számoljuk ki
3421548832 négyzetét zsebszámológép segítségével!
(A pontos értéket keressük.)
Feladat: 21.79. Megválaszthatók az előjelek a
kifejezésben úgy, hogy a kifejezés értéke
0 legyen? Oldjuk meg a
feladatot
a)
n=21
b)
n=20
c)
n=19
d)
n=18esetén!
Feladat: 21.80. Az asztalon fekszik egy papírlap. Ezt tíz részre téptük, majd az
egyik részt szintén tíz részre vágtunk. Így haladtunk tovább:
egy-egy lépésben mindig kiválasztottunk egy darabot és azt tízfelé
téptük. Lehetséges-e, hogy bizonyos számú lépés után
a) 201
b) 200
c) 199
darab papír lesz az asztalon?
Feladat: 21.81. Az asztalon fekszik egy papírlap. Ezt tíz vagy tizenhat részre
téphetjük; majd a kapott részek bármelyikét szintén tíz vagy
tizenhat részre vághatjuk. Ilyen lépések egymás utáni
alkalmazásával elérhetjük-e, hogy
a) 400
b) 399
a) 22
darab papír legyen az asztalon?
Feladat: 21.82. Két kupacban gyufák vannak. Egy-egy alkalommal valamelyik kupacba
beteszünk néhány szálat, s ugyanekkor a másik kupacba kétszer
annyit helyezünk. Elérhető-e, hogy mindkét kupacban 50 gyufaszál
legyen, ha kezdetben az egyes kupacokban
a)7
és 34
b) 1 és 3
szál gyufa volt.
Feladat: 21.83. Két kupacban gyufák vannak. Egy-egy alkalommal valamelyik kupacból
elveszünk néhány szálat, s a másik kupacba kétszer annyit
helyezünk. Elérhető-e, hogy mindkét kupacban ugyanannyi gyufaszál
legyen, ha kezdetben az egyes kupacokban
a)7
és 34
b) 1 és 3
szál gyufa volt.
Feladat: 21.84. Egy kocka csúcsaiba számokat írtunk. Egy-egy alkalommal valamelyik
él két végén álló számot 1-gyel növelhetjük. Ezt az eljárást
néhányszor megismételve elérhető-e, hogy minden csúcsban ugyanaz a
szám álljon, ha kezdő állapotban
a) az egyik csúcsban 1-es, a többiben 0 van;
b) az egyik él két csúcsában 1-es, a többi csúcsban 0
van;
c) az egyik lapátló két csúcsában 1-es, a többi csúcsban
0 van;
d) az egyik testátló két csúcsában 1-es, a többi csúcsban
0 van?
Feladat: 21.85. [
40] Egy tetraéder éleire felírtuk az 1, 2, 3, 4, 5, 6 számokat. Ezután
minden csúcsra elvégeztük a következő műveletet: az ide futó
éleken lévő számokat összeadtuk, és ráírtuk a csúcsra.
Kaphattunk-e a csúcsokon egyforma számokat?
Feladat: 21.86. [
80, 11.] Egy rét körül körben 44 fa áll, mindegyik fán egy-egy picinyke
cinke. Időnként két cinke egyszerre átrepül a szomszédos fára, de
mindig ellenkező irányba: az egyik az óra járása szerint
következőbe, a másik az óra járásával ellentétes irányba.
Bizonyítsuk be, hogy a cinkék így sose fognak összegyűlni
ugyanazon a fán.
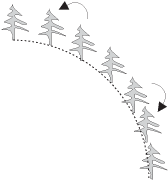
1. ábra
Mi a helyzet
n fa és
n cinke esetén?
Feladat: 21.87. Készítsük el az euklideszi algoritmus
struktogramját.
Feladat: 21.88. Gondolkodjunk el azon, hogy a számítógép hogyan ábrázolja
(ábrázolja-e egyáltalán) az irracionális számokat.





