2. FEJEZET: Mértani helyek I.
Feladat: 2.1. Az
A és a
B pont távolsága
10 cm. Milyen alakzatot alkotnak a síkban illetve a térben azok a pontok, amelyek
6 cm távolságra vannak
a) az
A ponttól;
b) az
AB egyenestől;
c) az
AB szakasztól;
d) az
A és a
B ponttól is;
e) az
{A,B} ponthalmaztól?
Feladat: 2.2. Az
A és a
B pont távolsága
10 cm. Szerkesszük meg azon pontok halmazát a síkon, amelyeknek az
A ponttól való távolsága legalább
a, míg a
B ponttól való távolsága pontosan
b, ha
a)
a=12 cm
b=3 cm;
b)
a=13 cm
b=3 cm;
c)
a=6 cm
b=3 cm!
Feladat: 2.3. Az
a és a
b egyenes szöge
60∘
. Szerkesszük meg azon pontok halmazát a síkon, amelyeknek az
a egyenestől való távolsága legalább
4 cm, míg a
b egyenestől való távolsága pontosan
2 cm!
Feladat: 2.4. A síkban dolgozunk. Vegyük fel az
e egyenest és tőle
5 cm távolságra a
P pontot. Szerkesszük meg és jelöljük az
A,
B,
C=A∩B halmazokat, ha
a)
A a
P ponttól legfeljebb
3 cm távolságra lévő pontok halmaza, míg
B az
e egyenestől legfeljebb
4 cm-re található pontok halmaza;
b)
A a
P ponttól legalább
3 cm távolságra lévő pontok halmaza, míg
B az
e egyenestől legfeljebb
9 cm-re található pontok halmaza;
c)
A a
P ponttól legfeljebb
10 cm távolságra lévő pontok halmaza, míg
B az
e egyenestől legalább
6 cm-re található pontok halmaza!
d)* Kíséreljük meg leírni a megfelelő ponthalmazokat a térben!
Feladat: 2.5. Vegyük fel az
5 cm sugarú
k kört és jelöljük különböző színekkel a
k-tól
1;
3;
5;
7;
cm távolságra elhelyezkedő pontok mértani helyét a
k kör síkjában! Írjuk le a megfelelő ponthalmazokat a térben!
Feladat: 2.6. A síkban dolgozunk. Vegyük fel az
5 cm sugarú
k kört és középpontjától
4 cm távolságra a
P pontot!
Hány olyan pont van, amely a
k körtől
dk
a
P ponttól
dP
távolságra van, ha
a)
dk
=2 cm
dP
=4 cm;
b)
dk
=2 cm
dP
=3 cm;
c)
dk
=6 cm
dP
=10 cm!
d) Legyen
dk
=2 cm és
dP
értékét futtassuk
0-tól
20 cm-ig! Írjuk le miképp változik a megfelelő
P pontok száma!
Feladat: 2.7. Adott egy
Σ sík és benne az
A pont és a
b egyenes.
Határozzuk meg azon
3 cm sugarú körök középpontjainak mértani helyét a
Σ síkban, amelyek
a) átmennek
A-n;
b) belsejükben tartalmazzák
A-t!
Határozzuk meg azon
3 cm sugarú körök középpontjainak mértani helyét a
Σ síkban, amelyek
c) érintik
b-t;
d) metszik
b-t!
Határozzuk meg azon
3 cm sugarú gömbök középpontjainak mértani helyét a térben, amelyek
e) átmennek
A-n;
f) belsejükben tartalmazzák
A-t!
Határozzuk meg azon
3 cm sugarú gömbök középpontjainak mértani helyét a térben, amelyek
g) érintik
b-t;
h) metszik
b-t!
Feladat: 2.8. Adott egy
Σ sík és benne az
5 cm sugarú
k kör.
Határozzuk meg azon
3 cm sugarú körök középpontjainak mértani helyét a
Σ síkban, amelyek
a) érintik
k-t;
b) metszik
k-t!
Határozzuk meg azon
6 cm sugarú körök középpontjainak mértani helyét a
Σ síkban, amelyek
c) érintik
k-t;
d) metszik
k-t!
Ne feledkezzünk meg róla és jelöljük is az a), c) feladatok megoldásában, hogy két kör úgy is érintheti egymást, hogy mindkettő a másik külsejében van, de úgy is, hogy az egyik a másik belsejében van!
Feladat: 2.9. a) Vegyünk fel az
A és a
B pontot egymástól
10 cm-re és szerkesszünk olyan
7 cm sugarú kört, amely mind a kettőn átmegy!
b) Legalább illetve legfeljebb mekkora lehet egy olyan kör sugara, amely az
A és a
B ponton is átmegy?
c) Hol lehet annak a
7 cm sugarú körnek a középpontja, amely a belsejében vagy a határán tartalmazza az
A és a
B pontot is?
d) Hol lehet annak a
7 cm sugarú körnek a középpontja, amely a belsejében vagy a határán tartalmazza az
A és a
B pontok közül legalább az egyiket?
Feladat: 2.10. a) Vegyük fel az egymást
45∘
-ban metsző
a,
b egyeneseket és szerkesszük meg az összes olyan
3 cm sugarú kört, amely mind a két egyenest érinti!
b) Legalább illetve legfeljebb mekkora lehet egy olyan kör sugara, amely az
a és a
b egyenest is érinti?
c) Hol lehet annak a
3 cm sugarú körnek a középpontja, amelynek van közös pontja az
a és a
b egyenessel is?
d) Hol lehet annak a
3 cm sugarú körnek a középpontja, amelynek az
a és a
b egyenesek közül legalább az egyikkel van közös pontja?
Feladat: 2.11. a) Vegyük fel az egymást
45∘
-ban metsző
a,
b egyeneseket és szerkesszük meg az összes olyan
3 cm sugarú kört, amely mind a két egyenest érinti!
b) Legalább illetve legfeljebb mekkora lehet egy olyan kör sugara, amely az
a és a
b egyenest is érinti?
c) Hol lehet annak a
3 cm sugarú körnek a középpontja, amelynek van közös pontja az
a és a
b egyenessel is?
d) Hol lehet annak a
3 cm sugarú körnek a középpontja, amelynek az
a és a
b egyenesek közül legalább az egyikkel van közös pontja?
Feladat: 2.12. A síkban dolgozunk. Adott az
e egyenes, tőle
4 cm távolságra az
O pont és adott még az
O középpontú
10 cm sugarú
k kör.
a) Szerkesztendő az összes olyan
2 cm sugarú kör, amely érinti
k-t is és
e-t is! Hány ilyen kör van?
b) Írjuk le, hogyan változik a
k-t és
e-t is érintő
r sugarú körök száma, ha
r értéke
0-tól
20 cm-ig nő!
Feladat: 2.13. Két adott ponttól -
A és
B - egyenlő távolságra lévő pontok mértani helyét keressük a síkban.
a) Szerkesszünk
10 ilyen tulajdonságú pontot!
b) Fogalmazzuk meg sejtésként, hogy mi lehet a keresett mértani hely!
c) Bizonyítsuk be a sejtést! Miért jó a b)-ben sejtett ponthalmaz minden pontja, és miért nem lehet másutt megfelelő pont?
d) Mi lehet a megfelelő mértani hely a térben?
Feladat: 2.14. Két adott metsző egyenestől -
a és
b - egyenlő távolságra lévő pontok mértani helyét keressük a síkban.
a) Szerkesszünk
10 ilyen tulajdonságú pontot!
b) Fogalmazzuk meg sejtésként, hogy mi lehet a keresett mértani hely!
c) Bizonyítsuk be a sejtést! Miért jó a b)-ben sejtett ponthalmaz minden pontja, és miért nem lehet másutt megfelelő pont? Gondoljunk a két egyenes által meghatározott mind a négy szögtartományra!
d) Mi két párhuzamos egyenestől egyenlő távolságra lévő pontok mértani helye a síkban?
Feladat: 2.15. Adott három pont. Szerkesztendő kör, amely átmegy mind a három ponton!
Hogyan függ az ilyen körök száma a pontok elhelyezkedésétől?
Feladat: 2.16. Adott három egyenes, amelyek közül semelyik kettő sem párhuzamos és nem mennek át mind egy közös ponton. Szerkesztendő kör, amely érinti mind a három egyenest!
Hány ilyen kör van?
Feladat: 2.17. Adott az egymást metsző
e és
f egyenes és
e-n az
E,
f-en az
F pont (lásd az
1. ábrát).
Olyan pontot keresünk, amely az
e-től ugyanolyan messze van, mint
ftől és
E-től ugyanolyan messze van, mint
F-től.
a) Írjuk le a szerkesztés menetét!
b) Hány ilyen pont van?
c) Függ-e a megoldások száma az
E,
F pontok elhelyezkedésétől?
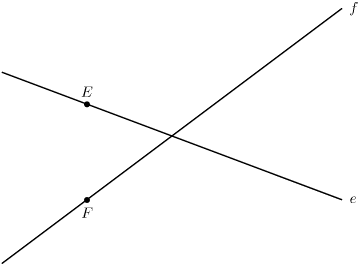
1. ábra
Feladat: 2.18. Adott a síkon az
A és a
B pont, melyek távolsága
10 cm. Válasszuk ki az alábbi állítások közül az igaz állításokat!
I. A síknak van olyan
P pontja, amelyre
PA<6 cm és
PB<7 cm.
II. Ha a sík valamely
P pontjára
PA<6 cm, akkor
PB<7 cm.
III. Ha a sík valamely
P pontjára
PA<6 cm, akkor
PB<17 cm.
IV. A síknak van olyan
P pontja, amelyre
PA<6 cm és
PB<17 cm.
V. A sík bármely
P pontjára teljesülnek a
PA<6 cm,
PB<17 cm egyenlőtlenségek.
VI. A sík bármely
P pontjára a
PA>6 cm,
PB>3 cm egyenlőtlenségek közül legalább az egyik teljesül.
VII. Ha a sík valamely
P pontjára
PA≤6 cm, akkor
PB≤3 cm.
VIII. Nincs a síkon olyan
P pont, amelyre
PA≤6 cm és
PB≤4 cm.
IX. Nincs a síkon olyan
P pont, amelyre
PA≤6 cm és
PB<4 cm.
Feladat: 2.19. Adott a síkon az
A és a
B pont, melyek távolsága
10 cm. Igaz-e az alábbi állítás?
Ha a sík valamely
P pontjára a
PA<6 cm és a
PB<4 cm feltétel is teljesül, akkor
P az
AB szakasz felezőpontja.
Feladat: 2.20. Adott a síkon az
A és a
B pont. Tudjuk, hogy igaz az alábbi állítás:
A sík bármely olyan
P pontjára, amelyre teljesül a
PA<2 cm egyenlőtlenség, teljesül a
PB<10 cm egyenlőtlenség is.
Mit állíthatunk az
AB távolságról?
Feladat: 2.21. Adott a síkon az
A és a
B pont. Tudjuk, hogy a következő állítás
nem igaz:
A sík bármely olyan
P pontjára, amelyre teljesül a
PA<2 egyenlőtlenség, teljesül a
PB>3 egyenlőtlenség is.
Mit állíthatunk az
AB távolságról?
Feladat: 2.22. a) A tanár felvette az
A és a
B pont a táblán, felírta a távolságukat is és megkérdezte Remek Robit:
- Igaz-e, hogy a tábla síkjának bármely olyan
P pontjára, amelyre teljesül a
PA>1 méter egyenlőtlenség, teljesül a
PB>3 dm egyenlőtlenség is?
Robi igennel felelt és a tanár megdícsérte a jó válaszért. Hunyor Hunor a besütő naptól nem látja a táblát és most hozzá fordul a tanár:
- Igaz-e, hogy a tábla síkjának bármely olyan
P pontjára, amelyre teljesül a
PA<4 dm egyenlőtlenség, teljesül a
PB<12 dm egyenlőtlenség is?
Tud-e biztos választ adni Hunor, anélkül hogy további információt kapna a két pont elhelyezkedéséről?
b) Módosítsuk a történetet úgy, hogy cseréljük ki a tanár két ,,Igaz-e, hogy... " kezdetű mondatát! Így tud-e Hunor biztos választ adni?
Feladat: 2.23. Kutyageometria
Egy hatalmas modern város utcahálózata olyan mint egy négyzetrács, melyben a négyzetek oldalának hossza
100 m. A kóbor kutyák csak az utcákon, azaz a négyzetrács vonalain közlekedhetnek, a házakba, azaz a négyzetekbe nem mehetnek be. A kutyák világa tehát a négyzetrács vonalainak világa. Két pont távolságán a két pont közötti rácsvonalakon haladó - a rácspontokban esetleg megtörő - töröttvonalak hosszának minimumát értjük. Ez a kutyageometria. Az
1. ábrán a város egy részének térképét látjuk.
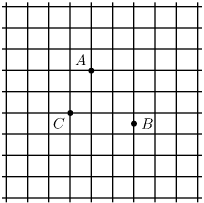
1. ábra
Határozzuk meg az
AB,
BC,
CA távolságokat!
Színezzük teli karikákkal, különböző színekkel az
A ponttól
b)
100;
c)
150;
d)
200;
e)
250;
f)
300;
méterre található pontok halmazát!
Színezzük üres karikákkal, különböző színekkel a
B ponttól
g)
100;
h)
150;
i)
200;
j)
250;
k)
300;
méterre található pontok halmazát!
Feladat: 2.24. Ebben a feladatban is a rácsvonalak ,,kutyageometriáját" vizsgáljuk (lásd a
2.23. feladatot). Körön, egy adott ponttól adott távolságra levő pontok halmazát értjük. Jelölje
k1
,
k2
és
k3
azt a kört, amelyeknek középpontja az
1. ábrán látható
O1
,
O2
illetve
O3
pont és amelynek sugara
r1
=100 m,
r2
=300 m,
r3
=500 m, ha egy rácsszakasz hossza
100 m.
Hány közös pontja van a
a)
k2
és
k1
;
b)
k1
és
k3
;
c)
k3
és
k1
;
köröknek?
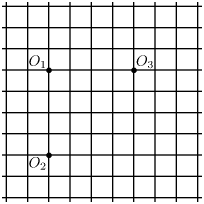
1. ábra
Feladat: 2.25. Ebben a feladatban is a rácsvonalak ,,kutyageometriáját" vizsgáljuk (lásd a
2.23. feladatot). Határozzuk meg az
1. ábrán látható
a)
A és
B;
b)
B és
C;
c)
C és
A;
pontoktól egyenlő távolságra lévő pontok halmazát!
d) Hány olyan pont van, amely egyforma messze van mind a három ponttól?
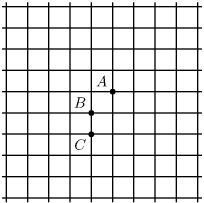
1. ábra
Feladat: 2.26. Ebben a feladatban is a rácsvonalak ,,kutyageometriáját" vizsgáljuk (lásd a
2.23. feladatot). Keressük három adott ponttól egyforma messze található pontok halmazát. Van-e három olyan pont, amelyre ennek a ponthalmaznak az elemszáma
a)
1;
b) végtelen;
c)
2?
Feladat: 2.27. Igaz-e a ,,kutyageometriában" (lásd a
2.23. feladatot) a háromszög egyenlőtlenség?
Feladat: 2.28. [
145] Lehet-e a ,,kutyageometriában" (lásd a
2.23. feladatot) két körnek (
2.24. feladat) éppen 13 metszéspontja?
Feladat: 2.29. [
118] Az ABC hegyesszögü háromszög
B csúcsára illeszkedö egyenesek közül melyiktől van az
AC oldal
F felezöpontja a legmesszebbre?
Feladat: 2.30. [
98] Simi kutyát kikötötték.
2 méter hosszú láncának karikája két - egymástól
10 méterre levő - fa között kifeszített drótkötélen csúszkálhat. Bobi kutyát szintén
2 méteres láncra kötötték egy cölöphöz.
Hová tűzhették Bobi kutya cölöpjét, ha a két kutya épp egy félkör alakú területen játszhat együtt?
Feladat: 2.31. A Kecskefy, a Kecsovszky és a Kecsora család is tenyészt kecskét. A három család másképp legelteti a kecskéket. Az állatokat nyakában található övre egy-egy 10 méter hosszú kötelet kötnek, de a kötél másik végén található gyűrűt különbözőképpen rögzítik.
Kecskefyék a réten egy
40×50 méteres téglalap csúcsaiban kitűznek egy-egy póznát, a póznák között pedig - a téglalap oldalain - kifeszítenek egy-egy drótot. A gyűrűk a póznákhoz vannak rögzítve, illetve szabadon futhatnak a drótokon két pózna között. A kecskék a téglalapon kívül és belül is mozoghatnak.
Kecsovszkyék csak a zöldségeskerten kívül engedik legelni a kecskéket. A kert háromszög alakú, oldalai 90, 100, 130 méter hosszúak. A kerítés mentén végigfutó dróton szabadon mozoghatnak a gyűrűk.
Kecsoráék külön tartják a kecskebakot, melynek gyűrűje egy rögzített póznához van kötve. A többi kecskén még kötél sincs, azok bárhol legelhetnek egy
40×80 m-es téglalap alakú zárt telken belül.
a) Készítsünk méretarányos rajzokat, feltüntetve azokat a részeket, ahol a kecskék legelhetnek!
b) Melyik család legelteti a legnagyobb területen a kecskéket?
Feladat: 2.32. Adott a síkon három pont. Szerkesztendő egyenes. amely ugyanolyan messze van mind a három ponttól. Hány ilyen egyenes van?
Feladat: 2.33. Adott a síkon négy pont. Szerkesztendő kör, amely ugyanolyan messze van mind a négy ponttól. Hány ilyen kör van?
Feladat: 2.34. Indiana Jones a Szent Kelyhet keresi. A Kehely a Titok Városának két sugárútja találkozása alatt van elrejtve. Jones éppen most találta meg Sir Galahad sírját, és benne az
1. ábra bal oldalán látható térképvázlatot. Feltételezhető, hogy a vázlat nem arányos a valósággal és nincs jól tájolva, de az elrendezés kereszt alakja biztosra vehető.
Indiana Jones édesapja fia rendelkezésére bocsátotta Oroszlánszívű Richárd írnokának jegyzeteit, amelyből az derült ki, hogy a Palota kapujának a Templom előtti kúttól való távolsága pontosan 800 méter.
A gonosz célból a Titok Városában ásatásokat folytató Ellenség éppen most talált meg egy kutat, amely feltehetően a Templom előtt állhatott.
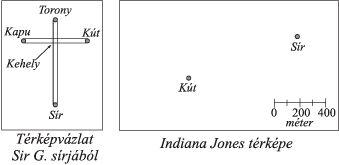
1. ábra
Indiana Jones térképvázlatot készít. Segítsünk neki! Szerkesszük meg a Kehely összes lehetséges helyét az
1. ábra jobb oldalán!
b) Indiana édesapja szerint a jegyzetben talált 800-as adat nem méterben értendő, hanem egy - a keresztes lovagok által használ - mára már elfeledett mértékegységben. Így mit lehet mondani, hol lehet a Kehely?
Feladat: 2.35. Ha megrajzoljuk a sík öt pontja közül mindegyik kettő felezőmerőlegesét, akkor a kapott egyenesek maximum hány pontban metszik egymást?





