3. FEJEZET: Speciális síkidomok
Feladat: 3.1. Az
1. ábrán az
AB,
BC,
CD,
BE és
EC szakaszok mind egyenlő hosszúak. Mekkora az
AED∠?
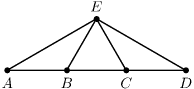
1. ábra
Feladat: 3.2. Egy
10∘
-os szög szárai közé, a szög
A csúcsából indulva berajzoltuk az
ABCDEF töröttvonalat, amelynek mindegyik oldala
1 cm
(lásd az
1. ábrát).
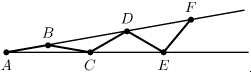
1. ábra
Mekkora az
AEF∠?
b) Meddig lehet folytatni a töröttvonalat?
c) És ha nem
1 cm-rel lépkedünk?
Feladat: 3.3. Mekkorák a szabályos hurkolt ötszög szögei (
1. ábra)?
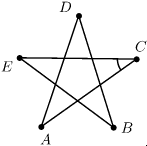
1. ábra
Feladat: 3.4. Adott a síkon az
ABC szabályos háromszög. Keressük meg a sík összes olyan
M pontját, amelyre az
ABM és az
ACM háromszög is egyenlő szárú!
Feladat: 3.5. Az
1. ábrán látható egyenlő szárú háromszögben a vastagon rajzolt szakaszok is egyenlőek. Mekkorák a háromszög szögei?

1. ábra
Feladat: 3.6. Az
ABC egyenlő szárú háromszög
BC szárán adott az
M, az
MC szakaszon pedig az
N pont úgy, hogy
MN=AN. Tudjuk, hogy a
BAM és az
NAC szögek egyenlőek. Határozzuk meg az
MAC∠ szög nagyságát!
Feladat: 3.7. Egy paralelogrammát az
1. ábrán látható módon lehet egyenlő szárú háromszögekre bontani. Mekkorák a paralelogramma szögei?
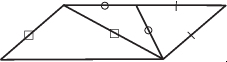
1. ábra
Feladat: 3.8. Mely háromszögek oszthatók fel egy egyenessel két egyenlő szárú háromszögre?
Feladat: 3.9. Egy téglalap egyik oldala
2 cm hosszú, egyik átlója pedig
4 cm-es. Mekkora szöget zárnak be az átlók az oldalakkal?
Megoldás: 3.9




