5. FEJEZET: Szimmetriák, transzformációk
Feladat: 5.1. Vegyük fel az
ABC háromszöget az alábbi adatokkal:
|
AB=8
cm
, AB=10
cm
, CA=4
cm
.
|
a) Szerkesszük meg a háromszög képét - az
A1
B1
C1
háromszöget - a
C-nél fekvő belső szög szögfelezőjére való tükrözésnél!
b) Határozzuk meg az
A1
B és az
AB1
szakaszok hosszát!
c) Fejezzük ki a b)-ben kérdezett szakaszok hosszát az általános esetben az
ABC háromszög oldalaival!
Feladat: 5.2. Vegyünk fel egy
ABC háromszöget az alábbi adatokkal:
|
BAC∠=
75∘
, CBA∠=
60∘
, BAC∠=
45∘
.
|
a) Szerkesszük meg a háromszög képét - az
A2
B2
C2
háromszöget, az
AB szakasz felezőmerőlegesére való tükrözésnél!
b) Határozzuk meg a
CAC2
∠ és
CBC2
∠ szögek nagyságát!
c) Fejezzük ki a b)-ben kérdezett szögeket az általános esetben az
ABC háromszög szögeivel!
Feladat: 5.3. Adottak az
A,
B,
C pontok. Szerkesztendő az
A pont
BC egyenesre vonatkozó tükörképe csak körzővel (tehát vonalzót az
AB egyenes meghúzásához sem használhatunk).
Feladat: 5.4. Szerkesszünk olyan
ABC háromszöget, melynek szögei:
|
CAB∠=
90∘
, BCA∠=
60∘
, ABC∠=
30∘
.
|
Tükrözzük a háromszöget egy-egy oldalára és vizsgáljuk az eredeti háromszög és képe egyesítéseként létrejött sokszöget.
Hány oldalú az így kapott sokszög és mekkorák a szögei? Válaszoljunk a kérdésre mind a három esetben (mind a három oldalra való tükrözés esetén)!
Feladat: 5.5. Vegyük fel az
ABC háromszöget az alábbi adatokkal:
|
AB=8
cm
, AB=10
cm
, CA=4
cm
.
|
a) Szerkesszük meg a háromszög képét az
AB szakasz
FC
felezőpontjára vonatkozó középpontos tükrözésnél!
b) Milyen alakzatot alkot a háromszög és képének egyesítése? Tegyünk megfigyelést, fogalmazzunk meg állítást és bizonyítsuk is be!
c) Tükrözzük középpontosan az eredeti háromszöget a
BC oldal
FA
és a
CA oldal
FB
felezőpontjára is!
d) Milyen alakzatot alkot az eredeti háromszög és három képének egyesítése? Tegyünk megfigyelést, fogalmazzunk meg állítást és bizonyítsuk is be!
Feladat: 5.6. Vegyük fel az
ABC háromszöget az alábbi adatokkal:
|
AB=8
cm
, AB=10
cm
, CA=4
cm
.
|
a) Szerkesszük meg a háromszög képét - az
A3
B3
C3
háromszöget - az
AB
→
vektorral való eltoláskor!
b) Milyen kapcsolat van az eredeti és a
CBC3
háromszög között?
Feladat: 5.7. Vegyük fel (két példányban) az
ABC szabályos háromszöget, annak
O középpontját, az
OB szakaszt és annak
F felezőpontját (a szerkesztést érdemes egy
O középpontú körrel kezdeni és azon megkeresni az
A,
B,
C pontokat).
Az alábbi szerkesztéseket az ábra egy-egy külön példányán végezzük el!
a) Forgassunk az
O középpont körül
60∘
-kal!
b) Forgassunk az
A csúcs körül
60∘
-kal!
Feladat: 5.8. Vegyük fel (három példányban) az
ABCD négyzetet, annak
O középpontját, az
OB szakaszt és annak
F felezőpontját (a szerkesztést érdemes egy
O középpontú körrel kezdeni és azon megkeresni az
A,
B,
C,
D pontokat).
Az alábbi szerkesztéseket az ábra egy-egy külön példányán végezzük el!
a) Forgassunk az
O középpont körül
45∘
-kal!
b) Forgassunk az
A csúcs körül
90∘
-kal!
Feladat: 5.9. Válasszuk ki a nagy nyomtatott magyar ABC betűiből a
a) tengelyesen szimmetrikusokat;
b) középpontosan szimmetrikusokat!
Feladat: 5.10. Szerkesszünk olyan hatszöget, amelynek nincs
60∘
-os forgási szimmetriája, de
120∘
-os forgási szimmetriája van!
Feladat: 5.11. Ketten játszanak - Kezdő és Második - felváltva helyeznek el pontokat a síkon, két menetben összesen négyet, minden menetben egyet-egyet.
Miután valamelyikük lerak egy pontot, a másik menetenként egyszer-egyszer mondhatja, hogy ,,ne oda tegyél" és akkor a pontot tevőnek másik helyet kell választania.
Második akkor nyer, ha a legvégül kapott pontrendszer
a) tengelyesen;
b) középpontosan
szimmetrikus lesz, egyébként veszít. Kinek van nyerő stratégiája?
Feladat: 5.12. Ebben a feladatban a végtelen sakktábla (lásd az
1. ábrát) szimmetriáit keressük.
Válasszuk ki, hogy az alábbi forgási szimmetriák közül melyekkel rendelkezik a végtelen sakktábla és jelöljük az ábrán a megadott színnel a megfelelő forgási szimmetriaközéppontokat!
a)
30∘
-os (sárga)
b)
45∘
-os (narancssárga)
c)
60∘
-os (zöld)
d)
90∘
-os (kék)
e)
120∘
-os (piros)
f)
180∘
-os (fekete).
g) Van-e a parkettázásnak szimmetriatengelye? Ha van jelöljük a tengelyeket!
h) Van-e olyan eltolás, amely minden parkettalapot egy másikba képez? Ha van jelöljük a megfelelő eltolásvektorokat!

1. ábra
Feladat: 5.13. Most a végtelen szabályos háromszögrács (lásd az
1. ábrát) szimmetriáit keressük.
Válasszuk ki, hogy az alábbi forgási szimmetriák közül melyekkel rendelkezik a végtelen sakktábla és jelöljük az ábrán a megadott színnel a megfelelő forgási szimmetriaközéppontokat!
a)
30∘
-os (sárga)
b)
45∘
-os (narancssárga)
c)
60∘
-os (zöld)
d)
90∘
-os (kék)
e)
120∘
-os (piros)
f)
180∘
-os (fekete).
g) Van-e a parkettázásnak szimmetriatengelye? Ha van jelöljük a tengelyeket!
h) Van-e olyan eltolás, amely minden parkettalapot egy másikba képez? Ha van jelöljük a megfelelő eltolásvektorokat!

1. ábra
Feladat: 5.14. Ebben a feladatban a sík
1. ábrán látható parkettázásának szimmetriáit keressük.
Válasszuk ki, hogy az alábbi forgási szimmetriák közül melyekkel rendelkezik a parkettázás és jelöljük a megadott színnel a megfelelő forgási szimmetriaközéppontokat!
a)
30∘
-os (sárga)
b)
45∘
-os (narancssárga)
c)
60∘
-os (zöld)
d)
90∘
-os (kék)
e)
120∘
-os (piros)
f)
180∘
-os (fekete).
g) Van-e a parkettázásnak szimmetriatengelye? Ha van jelöljük a tengelyeket!
h) Van-e olyan eltolás, amely minden parkettalapot egy másikba képez? Ha van jelöljük a megfelelő eltolásvektorokat!

1. ábra
Feladat: 5.15. Ebben a feladatban a sík
1. ábrán látható parkettázásának szimmetriáit keressük.
Válasszuk ki, hogy az alábbi forgási szimmetriák közül melyekkel rendelkezik a parkettázás és jelöljük a megadott színnel a megfelelő forgási szimmetriaközéppontokat!
a)
30∘
-os (sárga)
b)
45∘
-os (narancssárga)
c)
60∘
-os (zöld)
d)
90∘
-os (kék)
e)
120∘
-os (piros)
f)
180∘
-os (fekete).
g) Van-e a parkettázásnak szimmetriatengelye? Ha van jelöljük a tengelyeket!
h) Van-e olyan eltolás, amely minden parkettalapot egy másikba képez? Ha van jelöljük a megfelelő eltolásvektorokat!

1. ábra
Feladat: 5.16. Válasszuk ki M. C.Escher mester egyik parkettázását (lásd pl. a [
172][gallery/symmetry] weboldalt) és elemezzük szimmetriáit az
5.14-
5.15. feladatok mintájára!
Feladat: 5.17. Soroljuk fel az
1. ábra szimmetriáit!
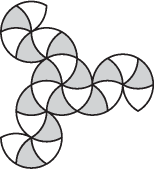
1. ábra
Feladat: 5.18. a) Parkettázzuk szabályos hatszögekkel a síkot!
b) Helyettesítsük az egyik szabályos hatszög egyik oldalát a hatszög körülírt körének megfelelő ívével és módosítsuk ennek és a többi parkettalapnak a többi oldalait úgy, hogy megmaradjanak a csúcspontok körüli
120∘
-os szimmetriák!
Feladat: 5.19. Adottak az
A pont, a
b egyenes, a
c kör és az
α szög. Szerkesztendő egyenlő szárú háromszög, amelynek az alappal szemközti csúcsa
A, míg a
B csúcs a
b egyenesen, a
C csúcs a
c körön van és a
BAC∠
a)
30∘
-os;
b) egy előre adott
α szöggel egyenlő.
Hány megoldása lehet a feladatnak?
c) Hány megoldás lehet, ha a
b egyenes helyett is egy kör adott, és azon kell elhelyezkednie a
B csúcsnak?
Segítség, útmutatás: 5.19
Először feledkezzünk meg arról, hogy a
C pontnak
c-re kell illeszkednie.
Vegyünk fel öt próbapontot
b-n:
B1
,
B2
,
B3
,
B4
és
B5
. Szerkesszük meg a hozzájuk tartozó
C1
,
C2
,
C3
,
C4
,
C5
pontokat úgy, hogy
ABi
Ci
olyan egyenlő szárú háromszög legyen, amelyben a szárak szöge
A-nál
60∘
(ill.
α). Tegyünk megfigyelést a
Ci
pontok elhelyezkedésére vonatkozólag!
Feladat: 5.20. Szerkesztendő rombusz, ha adott két átlójának egyenese és két
a) szomszédos;
b) átellenes
oldalának egy-egy pontja!
Segítség, útmutatás: 5.20
Hogyan tudnánk megszerkeszteni ugyanannak az oldalnak két különböző pontját?
A szimmetriatengely illetve a szimmetriaközéppont segít.
Feladat: 5.21. a) Szerkesztendő szimmetrikus trapéz (más szóval húrtrapéz), ha adott a szimmetriatengelye és mind a négy oldalának egy-egy pontja!
b) Határozzuk meg a trapéz csúcsainak koordinátáit, ha szimmetriatengelye az
y-tengely, míg a pontok az oldalain:
P(-2;3),
Q(3;2),
R(2;-4),
S(-3;-1)!
Feladat: 5.22. a) Szerkesztendő deltoid, ha adott két átlójának egyenese és három oldalának egy-egy pontja!
Határozzuk meg a deltoid csúcsainak koordinátáit, ha átlóinak egyenese a két koordinátatengely, míg három oldalának egy-egy pontja:
b)
P(-6;9)
Q(9;6)
R(6;-12);
c)
P(-6;9)
Q(9;6)
R(6;-3)
Hány ilyen deltoid van?
Feladat: 5.23. Adottak az
e,
b egyenesek, a
c kör és az
α szög. Szerkesztendő egyenlő szárú háromszög, amelynek
e a szimmetriatengelye,
B csúcsa a
b egyenesen,
C csúcsa a
c körön van és
BAC∠=α.
Hány megoldása lehet a feladatnak?
Feladat: 5.24. Szerkesztendő négyzet, ha adott egy
b kör és egy
d egyenes, amelyre rendre a
B illetve a
D csúcs illeszkedik valamint
a) az
AC átló egyenese;
b) az
A csúcs.
Feladat: 5.25. a) Adott az
O pont valamint az
a,
b,
c,
d egyenesek a síkon.
Szerkesztendő
ABCD paralelogramma, melynek
O a középpontja míg az
A,
B,
C,
D csúcsok rendre a megadott egyenesekre illeszkednek.
b) Adottak az
O,
P,
Q,
R,
S pontok a síkon.
Szerkesztendő
ABCD paralelogramma, melynek
O a középpontja a többi adott pont pedig a felsorolás szerint rendre az
AB,
BC,
CD,
DA oldal egyenesére illeszkedik.
Feladat: 5.26. Adott az
A és a
B pont valamint a
c és a
d kör a síkon.
Szerkesztendő olyan
ABCD trapéz, amelynek
CD alapja fele olyan hosszú, mint az
AB alap és
C,
D csúcsai rendre a
c,
d alakzatokra illeszkednek.
Feladat: 5.27. Adottak a
k1
,
k2
körök és az
e egyenes. Szerkesztendő olyan
e-vel párhuzamos
f egyenes, amelynek a két kör közé eső darabja
3 cm hosszú.
Feladat: 5.28. a) Adott az
O pont az
a egyenes és a
b kör. Szerkesztendő szabályos háromszög, melynek középpontja
O és
A,
B csúcsai rendre az
a,
b alakzatokra illeszkednek.
b) Adottak az
O,
Pa
,
Pb
pontok. Szerkesztendő az
ABC szabályos háromszög, melynek középpontja
O, míg
Pa
és
Pb
illeszkednek a háromszög
BC illetve
CA oldalegyenesére.
Feladat: 5.29. Szerkesztendő háromszög, ha adott két oldala és a harmadikhoz tartozó súlyvonala.
Segítség, útmutatás: 5.29
Lásd az
5.5. feladatot!
Feladat: 5.30. Szerkesztendő háromszög, ha adott
c oldala
α szöge valamint
a és
b oldalának különbsége.
Segítség, útmutatás: 5.30
Lásd az
5.1. feladatot!
Feladat: 5.31. Az
1. ábrán egy snooker (a billiárdhoz hasonló játék) asztal kicsinyített mása látható.
Az igazi tábla
3,6
m
×1,8
m
-es. Vegyük fel az asztal lapjának
10-szeresen kicsinyített képét és helyezzünk el egy-egy pontot a két golyónak megfelelően: a fehér golyó az asztal széltében és hosszában is a negyedelőpontban van az ábra szerint, míg a fekete golyó az asztal hosszának felénél, szélességének negyedénél helyezkedik el. Szerkesszük meg a fehér golyó útját, ha tudjuk, hogy
a) az
a oldalon való ütközés után;
b) a
b majd az
a oldalon való ütközés után;
c) a
c majd az
a oldalon való ütközés után
telibe találja a fekete golyót!
d) Számítsuk ki, hogy az
a oldalon a sarkoktól milyen messze pattan vissza a fehér golyó az egyes esetekben!
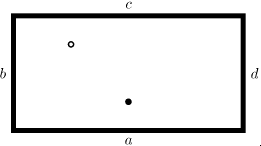
1. ábra
Feladat: 5.32. Adott egy téglalap (billiárd, snooker vagy pool asztal lapja) és benne két kör (a golyók). Szerkesszük meg az egyik falon azt a pontot, ahol az egyik golyónak ütődnie kell ahhoz, hogy visszapattanás után úgy lökje meg a másik golyót, hogy az az egyik sarok irányába menjen tovább!
Feladat: 5.33. Egy háromszög két oldalára kifelé négyzeteket rajzoltunk. Mutassuk meg, hogy az
1. ábrán a
DB,
AH szakaszok hossza egyenlő egymással!
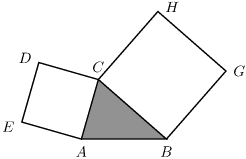
1. ábra
Feladat: 5.34. Adott egy négyzet. Mutassuk meg, hogy bármelyik egyenesnek a négyzet két párhuzamos oldalegyenese közé eső része és a rá merőleges egyenesnek a négyzet másik két oldalegyenese közé eső része azonos hosszúságú!
Feladat: 5.35. Adott a síkon az
A, a
B és a
C pont. Szerkesztendő olyan
C középpontú kör, amelynek (egyik)
A-t tartalmazó érintője merőleges az (egyik)
B-t tartalmazó érintőjére!
Feladat: 5.36. Adjunk meg olyan 10 pontból álló halmazt, amelynek pontosan
k darab szimmetriatengelye van. Mely
k nemnegatív egész szám esetén oldható meg a feladat? Adjunk mindegyik esetre példát! (Nem kell őket megszerkeszteni.)
Feladat: 5.37. Az
1. ábrán látható
75∘
-os körcikket elforgatjuk
75∘
-kal az óra járásával ellenkező forgásirányban. A kapott körcikket újból elforgatjuk
75∘
-kal, stb. Hányszor kell a forgatást elvégezni, hogy visszajussunk az eredeti körcikkhez?
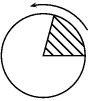
1. ábra
Feladat: 5.38. Az
ABC háromszög
AC oldalán adott a
P1
pont. Az
A pontba szúrt körzővel,
AP1
sugárral kört rajzolunk, ami a
P2
pontban metszi az
AB oldalt. Most a
B pontba szúrjuk a körzőt és
P2
-n keresztül húzunk egy kört (
BP2
sugárral), ami a
P3
pontban metszi az
CB oldalt. Így haladunk tovább, legközelebb a
C, majd újból az
A stb. ... pont körül körívezve.
Mit tapasztalunk? Fogalmazzunk meg állítást és próbáljuk meg igazolni!
Megoldás: 5.38







